独热编码
独热编码的概念
独热编码(one-hot)是解决无法量化类属性的优秀方法,其以简单高效的特点深受好评。例如我们在进行数据分类时会遇到一些特征:人的性别有男、女,人的国籍有中国,法国,德国....这些都是不能直接量化的变量。
假如使用[0,3]表示一个德国的男性,看似没有问题,实际 上是不可以的,这是因为如果德国表示3,那么中国表示1,法国为2。这就隐含了中国<德国,而这两者之间本身是不具备大小关系的,也不能进行简单的比较。这时我们就应当引入独热编码。
One-Hot编码,又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候只有一位有效。One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后,每个整数值被表示为二进制向量,除了整数的索引之外,它都是零值,它被标记为1。
以如上的引例为案例进行分析。男女由于有2个值,故可以采用2个二进制数进行表示,男为10,女为01,而国籍中假定只有三个国家,那么中国可以表示为100,法国为010,德国为001。(注意的是这与二进制的规律其实不太一样)。那么一个德国的男性用独热编码就可以写成10001,更清楚一点表示为10|001。
独热编码的意义
在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,基于的就是欧式空间。而我们使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。
独热编码在向量空间距离都相等,所以这样不会出现偏序性,基本不会影响基于向量空间度量算法的效果。
独热编码虽然解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间。但是当数据和属性量比较高时,会陷入高维的空间,此时对计算的时间和难度要求大大提高,这时可以通过PCA主成分分析或者CCA典型相关性分析进行维度的下降。
--------------------------------------------------------------
如果模型是基于参数的或者基于距离的优化,则一定要进行数据的预处理。基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 XGboost等。
独热编码的代码处理
采用scikit-learn方法作为脚本方法,其项目地址为:
import numpy as np
from sklearn.preprocessing import OneHotEncoder
def one_hot_encode(data, categories=None):
# 确保数据是二维数组形式
data_array = np.array(data).reshape(-1, 1)
if categories is not None:
encoder = OneHotEncoder(categories=[categories], sparse_output=False, handle_unknown='ignore')
else:
encoder = OneHotEncoder(sparse_output=False, handle_unknown='ignore') # 添加 handle_unknown='ignore'
encoded_data = encoder.fit_transform(data_array)
return encoded_data, encoder
"""
使用scikit-learn实现独热编码
参数:
data: 包含分类数据的列表或数组
categories: 可选,分类的列表。如果为None,则自动检测
返回:
编码后的数据和OneHotEncoder对象
"""使用说明如上。
特征选择工程
这里主要以特征选择的filter过滤法为主。
pearson相关系数
pearson相关系数是由卡尔.pearson从弗朗西斯.高尔顿在19世纪80年代提出的一个相似但稍有不同的想法演变来的,用于度量两个变量之间的线性相关程度,值介于-1和1之间。两个变量的pearson相关系数用它们的协方差与方差的商表示。
协方差的表示如下:
方差的表示如下:
那么,pearson系数的表示如下:
计算的流程:
计算变量x和y的均值\overline{x}\overline{y} 。
对每对观测值(x_i,y_i)计算各自与均值的差x-x_i,y-y_i。
计算这些差值的乘积之和。
分别计算这些差值的平方和。
最后:(步骤 3 的结果)除以(步骤 4 的结果的平方根)。
pearson相关系数的大小可以表示随机变量之间的相关程度和方向,如下表所示:
| 相关系数的大小范围 | 相关程度 | 相关方向 |
|---|---|---|
| 0.5 < r < 1 | 强相关 | 正向 |
| 0.3 <= r <= 0.5 | 中度相关 | 正向 |
| 0 < r < 0.3 | 弱相关 | 正向 |
| 0 | 不相关 | 无 |
| -0.3 < r < 0 | 弱相关 | 负向 |
| -0.5 <= r <= -0.3 | 中度相关 | 负向 |
| -1 < r < -0.5 | 强相关 | 负向 |
pearson相关系数的python实现代码如下:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
data = {
'a':[1, 2, 3, 4, 6, 10],
'b':[89, 100, 119, 150, 188, 200]
}
df = pd.DataFrame(data)
corr_matrix = df.corr(method='pearson')
print("pearson相关系数矩阵:")
print(corr_matrix)
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Correlation Matrix Heatmap')
plt.show()但是pearson相关系数的应用面实际上是十分狭窄的,他只能用于测量两个变量之间的线性关系。如果两个变量之间存在非线性关系,pearson相关系数可能无法准确反映其相关性。并且pearson相关系数在理想情况下,变量应当服从正态分布,或者至少满足对称分布。这在实际的生活中是很难达到的,这也限制了pearson相关系数的使用。更加广泛使用的而是spearman相关系数:
spearman相关系数
spearman相关系数是一种秩相关系数,这里的秩与矩阵的秩概念并不相同,其更指向的是一种排名的概念。这会在后文中提到。
spearman相关可以看作是pearson相关的非参数版本(nonparametric version)。pearson相关是关于两个随机变量之间的线性关系强度的统计度量(statistical measure),而spearman相关考察的是两者单调关系(monotonic relationship)的强度。计算pearson相关系数时使用的是数据样本值本身,而计算spearman相关系数使用的是数据样本排位位次值(有时候数据本身就是位次值,有时候数据本身不是位次值,则在计算spearman相关系数之前要先计算位次值)。
(这里的非参数可以认为是不需要像pearson相关系数那样严苛的数学条件,spearman相关性不严格要求正态分布,因此其实用性更强。)
而且pearson相关系数是异常点敏感的,异常点的影响对系数的影响非常大,但是异常点对spearman相关性的影响却是可以忽略不计的。
spearman相关系数的符号一般用ρ或者rs进行表示,其完整版本的计算公式如下:
其中R(x)表示的是x的位次,\overline{R(x_i)} 表示的是xi全体的平均位次。
但事实上,受限于原公式过于复杂,真正使用广泛的是下面的修正式:
其中di指的是第i个数据对的位次值之差,也即R(x)-R(y),n为总的观测样本数。
spearman相关系数的值在经过显著性检验后才能证明其具有说服力,一般来说若ρ的绝对值在0~0.5之间可以认为这两个变量之间几乎是没有关系的,然而当ρ的绝对值大于0.7后则需注意二者的关联度较大,有时需要删除一组属性才能对数据处理取得较好的成果(尤其是在进行主成分回归、偏最小二乘回归的时候),完整版的spearman相关性系数与样本总量的关系可以参考此网站:
https://www.docin.com/p-272983879.html
接下来,我们使用公式\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)}对具体的案例展开分析,假设我们有如下的数据集:
| ( x ) | ( y ) |
|---|---|
| 86 | 95 |
| 98 | 98 |
| 80 | 96 |
| 93 | 91 |
| 99 | 100 |
首先我们对数据集中的数据进行排序并依据大小赋秩次(如果有一类属性是负向属性,也就是说该属性中的值越大,效果反而是越差的,此时应该在数据的前面加上负号,也就是说秩次实际上是相反的!!!):
| ( x ) | ( y ) | ( R(x) ) | ( R(y) ) |
|---|---|---|---|
| 86 | 95 | 2 | 2 |
| 98 | 98 | 4 | 4 |
| 80 | 96 | 1 | 3 |
| 93 | 91 | 3 | 1 |
| 99 | 100 | 5 | 5 |
随后计算R(x)和R(y)的秩次差,如下表所示:
| ( x ) | ( y ) | ( R(x) ) | ( R(y) ) | ( d_i = R(x) - R(y) ) | ( d_i^2 ) |
|---|---|---|---|---|---|
| 86 | 95 | 2 | 2 | 0 | 0 |
| 98 | 98 | 4 | 4 | 0 | 0 |
| 80 | 96 | 1 | 3 | -2 | 4 |
| 93 | 91 | 3 | 1 | 2 | 4 |
| 99 | 100 | 5 | 5 | 0 | 0 |
接着我们计算它的秩次差的平方和:\sum d_i^2 = 0 + 0 + 4 + 4 + 0 = 8,取n=5,我们可以带入公式得到其spearman相关系数ρ=0.6。
其python实现的代码如下:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import spearmanr
# 使用您提供的表格数据
data = {
'x': [86, 98, 80, 93, 99],
'y': [95, 98, 96, 91, 100]
}
# 将数据转换为DataFrame
df = pd.DataFrame(data)
# 计算斯皮尔曼相关系数矩阵
corr_matrix = df.corr(method='spearman')
# 创建热力图
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix,
annot=True,
cmap='coolwarm',
center=0,
vmin=-1,
vmax=1,
square=True,
linewidths=.5,
cbar_kws={"shrink": .8})
# 添加标题和调整字体
plt.title("Spearman Rank Correlation (x vs y)", pad=20, fontsize=14)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
# 显示图形
plt.tight_layout()
plt.show()
# 也可以直接计算两列的斯皮尔曼相关系数
corr, p_value = spearmanr(df['x'], df['y'])
print(f"\n斯皮尔曼相关系数: {corr:.3f}")
print(f"P值: {p_value:.4f}")最后求得spearman相关性值为0.6,p的值为0.2848,热力图如下: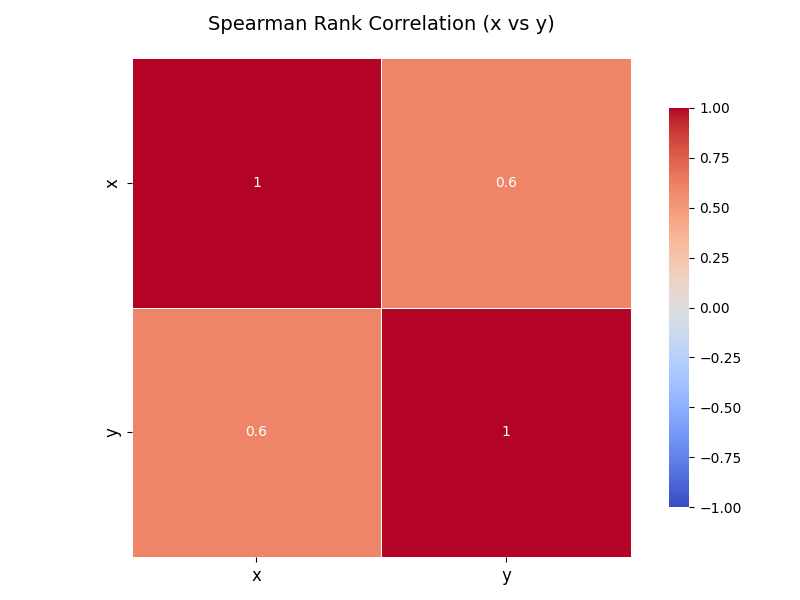
在变量非常多的时候,使用热力图效果更加明显。
Spearman相关性在数学建模中的应用场景
特征选择(Feature Selection)
在机器学习建模前,需要筛选与目标变量相关性强的特征。Spearman 相关系数可用于:
识别与目标变量具有单调关系的特征,即使不是线性关系。
适用于非线性数据(如指数、对数关系)。
(2) 变量相关性分析
在统计建模(如回归分析)中,Spearman 相关性可用于:
检测多重共线性(如果两个自变量高度相关,可能需要剔除一个)。
(3) 异常值检测
由于Spearman基于秩次,对异常值不敏感,可用于:
识别数据中的异常观测(如果Pearson相关性和Spearman相关性差异很大,可能存在异常值)。
(4) 时间序列分析
Spearman 相关性可用于:
分析趋势相关性(如股票A和股票B的价格是否长期同向变化)。
适用于非平稳时间序列(如存在趋势或周期性变化的数据)。


