DEA是一种用来衡量、评价效率的一种有效数学模型,是运筹学、数理经济学与管理科学交叉研究的一个新领域,它是根据多项投入指标和多项产出指标,利用线性规划的方法,对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法。
模型简介
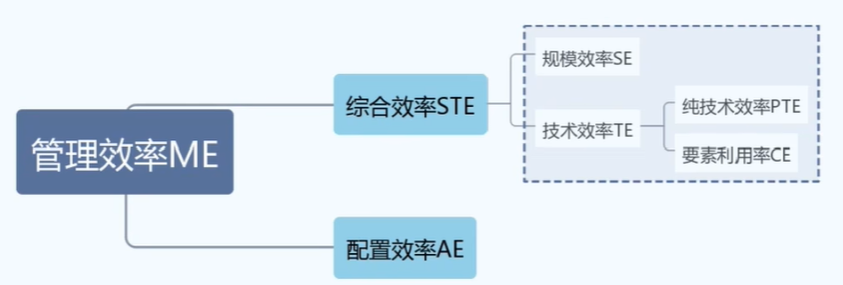
以公司的办事效率作为评判对象,进行数据包络分析的简介,一个公司的办事效率可以认为是由综合效率及配置效率所综合营私昂的,其中DEA模型所考虑的一般是综合效率及其影响因素,因为配置效率指的是一个公司通过提高装备等实现的效率增加,这与数据包络分析的主旨实质上是相违背的。
其中,
规模效率SE:指的是当生产要素同时增加了一倍,如果产量的增加正好是一倍,称之为规模报酬不变(-),如果产量增加多于一倍,则称之为规模报酬递增(irs),进而,如果产量增加少于一倍,就称为规模报酬递减(drs)
要素利用率效率CE:指在保持决策单元投入不变的情况下,实际产出同理想产出的比值。
首先简介几个名词:
决策单元(DMU):指具有相同类型的部门、企业或同一企业的不同时期等;在一定范围内通过一定数量生产要素产出一定数量的产出。
投入指标:指DMU在经济活动中需要耗费的经济量,如固定资产、流动资金、职工人数、占用土地等;
产出指标:指DMU的经济活动产生的成效,如销售收入、利税、产品数量、利润等;
指标数据:是指投入、产出指标的实际观测结果。
需要注意的是在进行投入变量和产出变量进行列表时,要注意正负相关性,例如:
| 方案 | 所需计算时间(秒) | 步骤数 | 精度(误差越小越好) | 是否通用(1表示通用) |
|---|---|---|---|---|
| A | 5 | 10 | 0.01 | 1 |
| B | 2 | 6 | 0.03 | 0 |
| C | 3 | 8 | 0.02 | 1 |
DMU很明显是A,B,C三个方案,输入指标是所需计算时间和步骤数,而输出变量则是精度的倒数和通用性。这里之所以说是精度的倒数是因为,精度越小越好,这与通用性越大越好是相反的,而输入变量中不需要进行这么多的考量则是因为其都是负相关的,因此可以并排展示。
正是由于要素利用率是在决策单元投入不变的情况下进行的,因此其恰好对应了DEA的一个分支(BCC)。
数据包络分析存在两个分支:CCR+BCC。其中CCR模型是指在以投入为导向时,要求产出效率不变,投入最小的一种方案,即STE(SE+TE)最小化;BCC模型是指在以产出为导向时,要求投入的效率不变,使产出最大化,即PTE最大化。
考虑到STE与PTE之间的关系,我们可以得到一个数学关系式。其中STE和PTE是可以通过两个基本的数学关系式所求出,故SE在一定条件下是可以确定的:
模型的数学建立
CCR模型:
设有n个DMU决策变量,每个DMU有m个输入变量和s各输出变量,不妨记第i个投入的权系数为v_i,第j个输出的权系数是u_j,那么第j个决策变量的输出综合为\vert\sum_{r=1}^{S}u_{r}\ \mathcal{y}_{rj},输入的综合为\sum_{i=1}^{m}v_{i}\ x_{i j},其效率评价指数Z_J可以表达为:
(输出的综合值除以输入的综合值)需要注意的是这里的权重一般都是自变量,需要后期我们通过非线性规划求解出一批最佳的权重,从而确定其值。
可以用如下的图来表示这一定义的过程: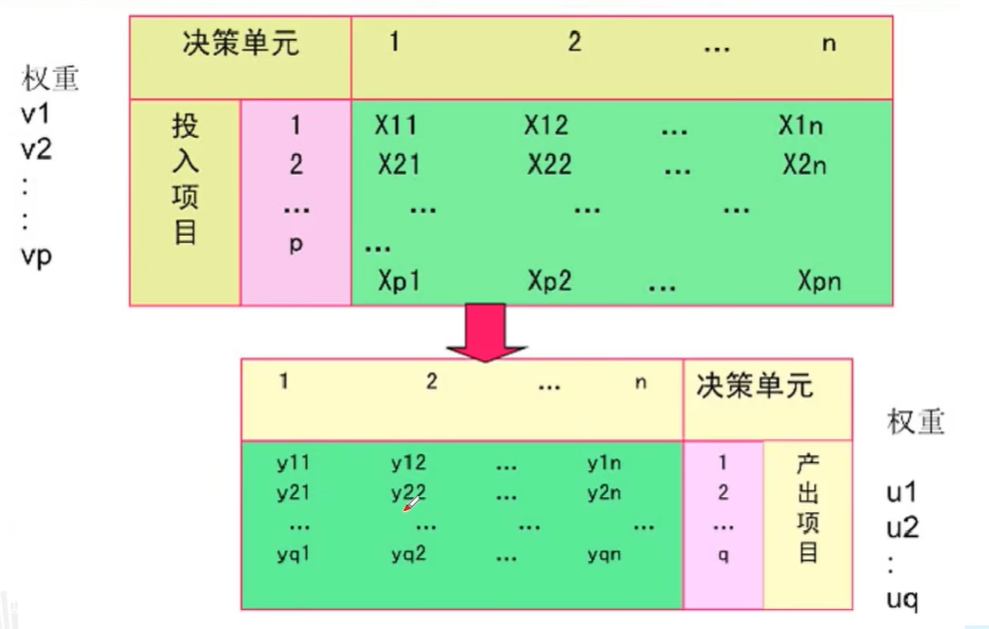
其中我们要对每一个DMU建立一个规划方程,求解对于其最佳的一批权重值,其方程如下:(其中角标j0表示的是不同DMU的效率评价指数)
另外对于每一个Z_{j0}我们都要限制其小于等于1,这是因为效率不能超过100%!
由于上述方程为非线性规划方程,在使用matlab/lingo求解难度和精度上是很难保证的,因此我们可以采用如下变量换元变化,使原非线性规划转变为线性规划方程:t=\frac{1}{\Sigma_{i=1}^{m}\,v_{i}\;x_{i j}}\;,\;\;\;\mu_{r}=t u_{r},\;\;\omega_{i}=t v_{i},\;\;.,化简后原分式规划方程简化为如下的线性规划:
我们再考虑构造其对偶问题,以简化计算求解的时间复杂度:
BCC模型
在报酬固定的情况下,DMU满足\sum_{j=1}^{n}\lambda_{j}=1,消除规模效率SE的影响,即可得到关于PTE的BCC模型,其也是一个线性规划模型:
DEAP软件对DEA模型的求解
由于DEA模型的求解涉及大量线性规划问题,在求解的难度上是极高的。最初的开发人员在20世纪末便研发出了DEAP.exe以实现对DEA数据包络模型的快速求解,软件下载的地址:
完成解压之后,在进行deap.exe之前,首先对dta.txt文件进行编辑,以行数代表DMU,列数代表输入变量+输出变量;
随后打开ins.txt,详细解释见如下的代码区域
eg1-dta.txt DATA FILE NAME 数据来源的文件名称
eg1-out.txt OUTPUT FILE NAME 期望输出报告的文件名称
5 NUMBER OF FIRMS 决策单元DMU的数量
1 NUMBER OF TIME PERIODS 时期检验,一般不需要修改,保留值为1即可
1 NUMBER OF OUTPUTS 输出变量的列数
2 NUMBER OF INPUTS 输入变量的列数
0 0=INPUT AND 1=OUTPUT ORIENTATED 0表示投入主导型,类似于CCR,1表示产出主导型,类似于BCC
0 0=CRS AND 1=VRS CRS表示规模收益固定模型,VRS表示规模收益可变模型(详细解释见后)
0 0=DEA(MULTI-STAGE), 1=COST-DEA, 2=MALMQUIST-DEA, 3=DEA(1-STAGE), 4=DEA(2-STAGE) 算法逻辑,默认为0关于规模与收益固定和可变是存在巨大差异的,具体如下图所示:
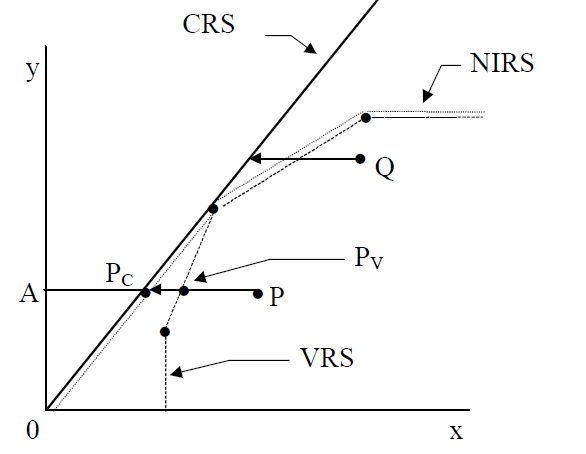
CRS如实线所示,其y与x的斜率是一个定值,表示规模收益固定,而VRS如图中虚线所示,表示的是规模和收益是可变的模型。
随后进入DEAP.exe在终端下输入ins.txt即可输出数据报告。其部门截图如下:
| firm | crste | vrste | scale | |
|---|---|---|---|---|
| 1 | 0.500 | 1.000 | 0.500 | irs |
| 2 | 0.500 | 0.625 | 0.800 | irs |
| 3 | 1.000 | 1.000 | 1.000 | - |
| 4 | 0.800 | 0.900 | 0.889 | drs |
| 5 | 0.833 | 1.000 | 0.833 | drs |
其中crste表示的是STE值,vrste表示的是PTE值,scale表示的是SE值。
而drs和irs则表示的是其相对于固定规模效益时的变化情况。
使用DEA模型我们可以考虑当一个问题出现多种解决方案时,利用其判断某个解决方案的优劣程度。
CCR与BCC的局限性
由于CCR模型和BCC模型都是径向模型,在径向模型中,效率改善主要指的是投入或产出的等比例线性缩放,同时忽略了平行于坐标轴的弱有效的情形,而SBM模型纳入无效率的松弛改进(即输入、输出的剩余冗余或不足),保证最终的结果是强有效的。SBM 模型直接把输入冗余和输出不足(松弛变量)纳入效率计算,能更真实反映 DMU 的效率。
非期望SBM模型的数学建立
其数学表达式如下(部分表达式的含义与CCR模型及BCC模型中的相同)
其中目标函数ρ^{*}表示效率值,该模型同时从投入和产出两个方面考察无效率的表现,故称为非径向模型。由于该模型为非线性模型,将该模型转化为线性模型,同时向模型中加入非期望产出得:
其中对于每一个决策单元k=1,2,3...。该模型中包含投入矩阵X_{n*m}的转置,期望产出矩阵{Y^g}_{n \times s_1} 的转置,非期望产出{Y^g}_{n \times s_2} 的转置,模型参数主要包括投影变量\Lambda,松弛变量S^{-},S^{a}S^{b} 和t。
实例解析
某市教委需要对六所重点中学进行评价,其相应的指标如表所示。表中的生均投入和非低收入家庭百分比是输入指标,生均写作得分和生均科技得分是输出指标。请根据这些指标,评价哪些学校是相对有效的。
| 学 校 | ( A ) | ( B ) | ( C ) | ( D ) | ( E ) | ( F ) |
|---|---|---|---|---|---|---|
| 生均投入(百元/年) | 89.39 | 86.25 | 108.13 | 106.38 | 62.40 | 47.19 |
| 非低收入家庭百分比 (%) | 64.3 | 99 | 99.6 | 96 | 96.2 | 79.9 |
| 生均写作得分(分) | 25.2 | 28.2 | 29.4 | 26.4 | 27.2 | 25.2 |
| 生均科技得分(分) | 223 | 287 | 317 | 291 | 295 | 222 |
根据以上的分析,其相关的matlab代码如下:
%非期望产出SBM模型
clc,clear
X=[89.39 86.25 108.13 106.38 62.4 47.19;
64.3 99 99.6 96 96.2 79.9];
Y=[25.2 28.2 29.4 26.4 27.2 25.2;
223 287 317 291 295 222];
Z=[72 85 95 63 81 70]; %非期望产出:生均艺术得分
[m,n]=size(X);
s1=size(Y,1);
s2=size(Z,1);
c=1/(s1+s2);
rho=[];
w=[];
for i=1:n
f=[-1./(m*X(:,i)') zeros(1,s1) zeros(1,s2) zeros(1,n) 1];
A=[];
b=[];
UB=[];
LB=zeros(m+s1+s2+n+1,1);
Aeq=[zeros(1,m) c*1./Y(:,i)' c*1./Z(:,i)' zeros(1,n) 1;
eye(m) zeros(m,s1) zeros(m,s2) X -X(:,i);
zeros(s1,m) -eye(s1) zeros(s1,s2) Y -Y(:,i);
zeros(s2,m) zeros(s2,s1) eye(s2) Z -Z(:,i)];
beq=[1 zeros(m,1)' zeros(s1,1)' zeros(s2,1)'];
[w(:,i),rho(i)]=linprog(f,A,b,Aeq,beq,LB,UB);
end
rho'


