MATLAB实现模拟退火算法：从原理入门到求解TSP问题实战

模拟退火算法（Simulated Annealing）是一种启发式优化算法，灵感来源于固体退火过程中的原子热运动。它通过模拟高温下原子随机运动及逐渐冷却稳定的过程，在解空间中探索最优解。算法以一定概率接受劣质解，避免陷入局部最优，逐步降低“温度”参数，收敛至全局最优或近似最优解。适用于复杂的非线性、多峰函数优化问题。

一、背景介绍

模拟退火的思想源于固体退火过程。在物理学中，退火是一种金属热处理工艺，通过将材料加热至高温后缓慢冷却，使其原子从高能态逐渐趋于稳定，最终形成低能态的晶体结构。这一过程启发了科学家将物理现象与优化问题联系起来。
模拟退火算法由Kirkpatrick、Gelatt和Vecchi在1983年首次提出，并发表在《Science》杂志上。他们借鉴了Metropolis等人于1953年提出的蒙特卡洛方法，将其应用于组合优化问题。通过引入“温度”参数和概率性接受劣解的策略，模拟退火算法能够有效跳出局部最优，寻找全局最优解。

二、基本原理

（1）算法的物理背景

如果用粒子的能量定义材料的状态，Metropolis 算法用一个简单的数学模型描述了退火过程。假设材料在状态i之下的能量为Ei，那么材料在温度T 时从状态i进入状态j 就遵循如下规律：

1. 如果E(j)\leq E(i),接受该状态被转换。

2. 如果E(j)>E(i),则状态转换以如下概率被接受：e^{\frac{E(i)-E(j)}{KT}}，其中 K 是物理学中的波尔兹曼常数，T 是材料温度。

   在某一个特定温度下，进行了充分的转换之后，材料将达到热平衡。这时材料处

   于状态i 的概率满足波尔兹曼分布：P_T(x=i)=\frac{e^{\frac{E(i)}{KT}}}{\sum_{j\in S}e^{\frac{E(j)}{KT}}}其中 x 表示材料当前状态的随机变量， S 表示状态空间集合。

   显然：\lim_{T\to\infty}\frac{e^{-\frac{E(i)}{KT}}}{\sum_{j\in S}e^{-\frac{E(j)}{KT}}}=\frac{1}{\mid S\mid}其中|S|表示集合S中状态的数量。

     这表明所有状态在高温下具有相同的概率，而当温度降低时，有

   \underset{T\to 0}{\mathop{\lim }}\,\frac{{{e}^{-\frac{E(i)-{{E}_{\min }}}{KT}}}}{\sum\limits_{j\in S}{{{e}^{-\frac{E(j)-{{E}_{\min }}}{KT}}}}}=\underset{T\to 0}{\mathop{\lim }}\,\frac{{{e}^{-\frac{E(i)-{{E}_{\min }}}{KT}}}}{\sum\limits_{j\in {{S}_{\min }}}{{{e}^{-\frac{E(j)-{{E}_{\min }}}{KT}}}}+\sum\limits_{j\in {{S}_{\min }}}{{{e}^{-\frac{E(j)-{{E}_{\min }}}{KT}}}}}\text{ }

其中{{E}_{\min }}=\underset{j\in S}{\mathop{\min }}\,E(j){{S}_{\min }}=\{i\mid E(i)={{E}_{\min }}\}，上式表明当温度降至很低时，材料会以很大概率进入最小能量状态。

(2).模拟退火背后的数学逻辑：

考虑这样一个组合优化问题：优化函数为f:x\to {{R}^{\text{+}}}，其中x\in S，他表示优化问题的一个可行解，{{R}^{+}}=\{y\mid y\in R,y>0\}，S表示函数的定义域，N\text{x}\subseteq S表示x的一个邻域集合。

首先给定一个初始温度 T0 和该优化问题的一个初始解x(0)，并由x(0)生成下一个解x'∈ N(x(0))，是否接受x'作为一个新解x(1)依赖于下面概率：

换句话说，如果生成的解x'的函数值比前一个解的函数值更小，则接受x(1) = x'作为一个新解。否则以概率e^{\frac{E(i)-E(j)}{KT}}接受x'作为一个新解。

除了给定的初值，我们还可以把他推广到x(k)到x(k+1)的马尔科夫过程，即在的基础上接受为

在温度{{T}_{i}}，经过很多次的转移之后，降低温度{{T}_{i}},得到{{T}_{i\text{+}1}}<{{T}_{i}}。在{{T}_{i\text{+}1}}下重复上述过程。因此整个优化过程就是不断寻找新解和缓慢降温的交替过程。最终的解是对该问题寻优的结果。

三．模型实施步骤

模拟退火算法可以分解为熔解过程、等温过程和冷却过程。熔解过程主要是初始化控制参数。{{T}_{0}}、获取初始解状态{{X}_{1}}，每个T值的迭代次数L；等温过程主要是通过状态转移函数获取{{X}_{2}}、使用Metropolis采样接受准则接受或者舍弃{{X}_{2}}；冷却过程主要是使用温度冷却函数降低控制参数T.

1. 初始化：设置初始温度{{T}_{0}}(充分大）、初始解状态{{X}_{1}}1.     (（是算法迭代的起点）、每个T值的迭代次数L

2. 使用状态转移函数产生新解{{X}_{2}}

3. 计算增量\text{ }\!\!\Delta\!\!\text{ }E=E(X2)-E(X1),其中E(X)为评价函数

4. 若\text{ }\!\!\Delta\!\!\text{ }E<0，则接受{{X}_{2}} 作为新的当前解，否则以概率e^{\frac{E(i)-E(j)}{KT}} 接受{{X}_{2}} 作为新的当前解（此为Metropolis采样稳定判断准则）

5. 如果控制参数T满足终止条件，则输出当前解作为最优解，结束程序

6. 如果不满足终止条件，逐渐减小T转第2步。

四、应用场景

模拟退火算法的应用领域十分广泛，包括但不限于：

（1）旅行商问题（TSP）：寻找最短路径，使得旅行商访问所有城市并返回起点。

（2）车辆路径问题（VRP）：优化配送路线，降低运输成本和时间。

五、实证分析

典型的TSP旅行商问题：给出了以下5个城市的坐标，且假设各个城市之间都是相通的，请找出一条访问一组城市并返回起点的最短路径，且每座城市只能访问一次。

（1）确定空间和目标优化函数.解空间S可表示为\left\{ 1,2,3,4,5 \right\}的所有终点与起点的集合，即S=\left\{(\pi_1...\pi_5),\text{其为}1{\sim}5\text{的循环排列,}\right\}这里可以先用蒙特卡诺放阀求得一个比较好的初始解。目标函数记为经过所有目标城市的路径长度最短，于是有\min f({{\pi }_{1}},{{\pi }_{2}}\ldots {{\pi }_{5}})=\sum\limits_{i=1}^{5}{{{d}_{{{\pi }_{i}}{{\pi }_{i+1}}}}}

（2）优化的思路。很显然我们要将路程最短，于是我们可以构造代价函数差，用来衡量2中方法的优良，即\Delta f=(d_{\pi_{u-1}\pi_\nu}+d_{\pi_u\pi_{\nu+1}})-(d_{\pi_{u-1}\pi_u}+d_{\pi_\nu\pi_{\nu+1}})，接受准则为：

如果Δf < 0，则接受新的路径。否则，以概率{{\text{e}}^{-\frac{\Delta f}{T}}}接受新的路径，即用计算机产生一个[0,1]区间上均匀分布的随机数rand，若rand\leq\mathrm{e}^{\frac{\Delta f}{T}}则接受。

（3）模拟退火算法的确定。我们可以选取初始温度1000，以降温系数 =0.95进行降温，即新的温度为\alpha T，选择最终的停止温度为{{10}^{\text{-}30}}，判断退火过程是否结束，如果温度低于{{10}^{\text{-}30}} ，我们认为全局最优解已经找到。

  很明显，如果初始温度的设定越高，停止温度的设定越低，降温速率的设定越慢，我们得到的最优解会越精准，但在这同时计算资源和计算时间的消耗会更高。

上述求解步骤的MATLAB代码如下：

% 设置模拟退火参数
temperature = 1000;
cooling_rate = 0.95;
final_temperature = 1e-30;

% 城市坐标
cities = [1, 2; 3, 4; 5, 6; 7, 8; 9, 10];

% 计算总距离
calc_distance = @(sol) sum(sqrt(sum(diff([sol; sol(1, :)]).^2, 2)));

% 生成随机解
gen_random_solution = @(cities) cities(randperm(size(cities, 1)), :);

% 模拟退火算法
function best_solution = simulated_annealing(cities, temperature, cooling_rate, final_temperature)
    current_solution = gen_random_solution(cities);
    best_solution = current_solution;
    best_distance = calc_distance(best_solution);
    
    while temperature > final_temperature
        neighbor_solution = gen_random_solution(cities);
        neighbor_distance = calc_distance(neighbor_solution);
        
        if neighbor_distance < best_distance || rand < exp((best_distance - neighbor_distance) / temperature)
            best_solution = neighbor_solution;
            best_distance = neighbor_distance;
        end
        
        temperature = temperature * cooling_rate;
    end
end

% 运行模拟退火算法
best_solution = simulated_annealing(cities, temperature, cooling_rate, final_temperature);

% 输出最优解
disp('最优解：');
disp(best_solution);
disp(['最优距离：', num2str(calc_distance(best_solution))]);

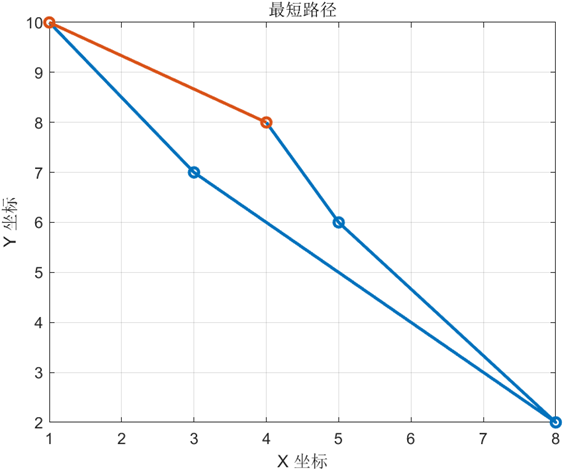
最后得到的最短路径如图所示：

六、方法评价

（1）优点：

• 能够跳出局部最优：通过 Metropolis准则（接受较差解的概率取决于温度），SA 可以在搜索过程中逃离局部最优，逐步逼近全局最优解；

• 适用于大规模复杂优化问题：SA 不需要问题有特定的数学结构（如可微性、凸性），适用于离散优化和连续优化问题；

（2）缺点：

• 收敛速度较慢：退火过程需要逐步降低温度，尤其是在低温阶段，需要较长时间才能达到收敛；

• 参数敏感：在退火速率、初始温度、终止温度等参数需要经验或试验调整，不同参数会显著影响算法效果；

• 可能收敛到次优解：如果降温过快或邻域搜索策略不合理，SA 可能未充分探索解空间，从而收敛到次优解。

七、拓展阅读

模拟退火是一种仿生优化算法，源于金属退火过程，通过模拟高温状态下原子自由运动、逐渐冷却后趋于稳定的机制来求解最优解。SA 以随机搜索为基础，结合温度控制策略，使算法在初期具备较强的探索能力，可接受较差解以跳出局部最优，随着温度下降，逐步向全局最优收敛。该算法适用于求解旅行商问题（TSP）、生产调度、机器学习超参数优化等复杂优化问题。学习者可深入研究不同退火策略（如几何退火、对数退火）对算法性能的影响，以及邻域搜索方式（如交换、逆转、插入）在不同场景下的适用性。此外，SA 可与遗传算法（GA）、禁忌搜索（TS）等方法结合，提高搜索效率与收敛精度。在实际应用中，合理调整初始温度、冷却速率等参数至关重要，以确保算法兼顾搜索空间的广度与局部优化能力。