以生活中常见的超市购物为例,我们熟知的啤酒与尿布故事是指某超市在对顾客购物习惯分析时,发现,男性顾客在购买婴儿尿片时,常常会顺便搭配几瓶啤酒来犒劳自己,于是尝试推出了将啤酒和尿布摆在一起的促销手段,最后使得啤酒与尿布销量双双提升。这是因为啤酒与尿布之间存在某种巧妙的相互关联,这种关联使得二者容易同时出现。
关联分析问题的数学建模
在以下的实际实例中,一个样本被称为一个事务,而每个事务是由多个属性来共同决定的,这里的属性被称为叫做“项”。而由多个项组成的集合被称为叫做“项集”。
| 编号 | 牛奶 | 果冻 | 啤酒 | 面包 | 花生酱 |
|---|---|---|---|---|---|
| T₁ | 1 | 1 | 0 | 0 | 1 |
| T₂ | 0 | 1 | 0 | 1 | 0 |
| T₃ | 0 | 1 | 1 | 0 | 0 |
| T₄ | 1 | 1 | 0 | 1 | 0 |
| T₅ | 1 | 0 | 1 | 0 | 0 |
| T₆ | 0 | 1 | 1 | 0 | 0 |
| T₇ | 1 | 0 | 1 | 0 | 0 |
| T₈ | 1 | 1 | 1 | 0 | 1 |
| T₉ | 1 | 1 | 1 | 0 | 0 |
为了方便后面的描述,我们会对一个项集中所包含的元素数目对项集进行分类,例如:{牛奶},{面包}都是1-项集,而{牛奶,面包}则变成了2-项集,同样的如果{。。。。。。。}中有k个属性,则被称为k-项集。
需要注意的是,在市场的关联规则挖掘中事务是顾客一次购物所购买的物品,但事务中是并不包含这些商品的具体信息,例如商品的数量、价格等。
我们常用数学符号X==>Y来描述X与Y项集之间的关联性,其中X被称为规则前项,Y被称为规则后项。
为了更好的描述项集X与项集Y之间的关联程度,我们引入了支持度,置信度和提升度三个函数来衡量这一抽象的概念。
支持度:一个项集在所有的事务中出现的频率。(需要注意我们在这对所有的计算都是按照出现的编号个数以频率代替概率的形式呈现的,而不是数其他的东西。)
利用项集规则X==>Y表示物品集X和物品集Y同时出现的概率,其中\sigma(X)表示的是二者同时出现的计数,N表示的是所有物品集出现的总数。
置信度:确定Y在包含X的所有事务中的出现概率(类似于条件概率)
其中p(XY)表示的是X和Y同时出现的概率。
在实际的计算中,我们一般会在程序运行之前设定置信度和支持度的阈值,即最小置信度和最小支持度,只有超过这一阈值的关联规则才会被保留,这种规则一般称为强关联规则,如果某规则的置信度和支持度小于阈值则在计算的之后这一项集会被自动地舍弃,这种被称为叫做弱关联规则。
提升度:物品集A的出现对物品B出现的概率发生了多大的改变。
提升度的提出是为了改进置信度的漏洞,假如现在有1000个消费者,有500人购买了茶叶,其中有450人同时购买了咖啡,另50人没有。由于置信度(茶叶=>咖啡)=450/500=90%,由此可能会认为喜欢喝茶的人往往喜欢喝咖啡。但如果另外没有购买茶叶的500人,其中同样有450人购买了咖啡,同样是很高的置信度90%,由此,得到不爱喝茶的也爱喝咖啡,这与原来的结论是背道而驰的。这样看来,其实是否购买咖啡,与有没有购买茶叶并没有关联,两者是相互独立的,其提升度90%/[(450+450)/1000]=1。
一般来说如果提升度的值等于1,则认为X与Y是相互独立的,X的出现对Y的出现不会带来任何的提升作用,而当提升度大于1并且增加的时候,则表明X对Y的提升程度越大,也表明关联性越强。
| 交易ID | 购买的商品 |
|---|---|
| 1 | A,B,C |
| 2 | A,C |
| 3 | A,D |
| 4 | B,E,F |
例如在上出现的例子中,如果假设最小支持度和最小置信度都是50%,则A==>C的支持度为\frac{2}{4}=0.5,而A==>C的置信度为\frac{2}{3}=0.667,提升度为0.3333,同理可以得到C==>A的支持度为50%,置信度为100%,提升度为3。由这个例子我们可以发现如果规则前项与规则后项互换顺序,最终得到的置信度,支持度和提升度都是不一样的!!
Apriori+PCY算法解决关联分析问题
Apriori算法
获得频繁项集,最简单直接的方法就是暴力搜索法,但是这种方法计算量过于庞大,如下图所示,k项的数据集可能生成 2^{k-1}个项集。
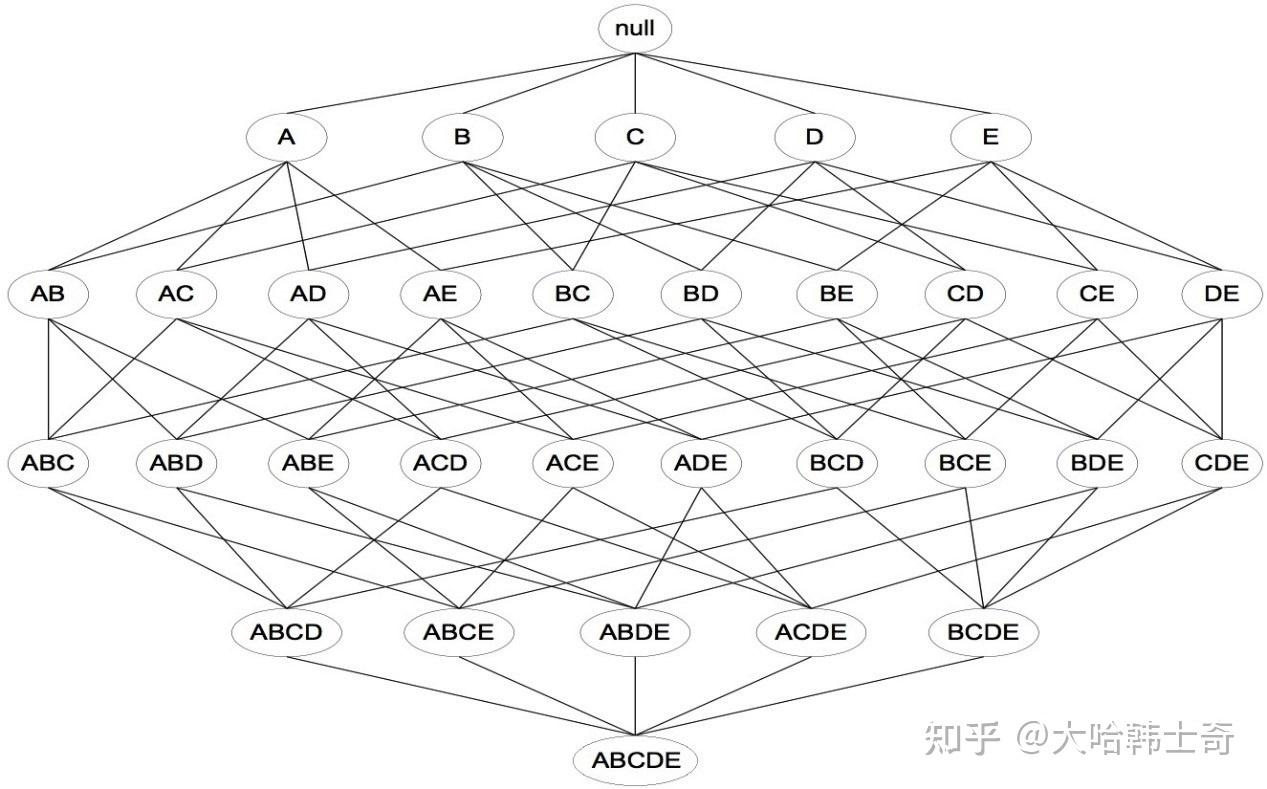
可见(暴力搜索)Brute-force在实际中并不可取。必须设法降低产生频繁项集的计算复杂度。此时可以利用支持度对候选项集进行剪枝,这也是Apriori算法所利用的第一条先验原理:
Apriori定律1:如果一个集合是频繁项集,则它的所有子集都是频繁项集。 例如:假设一个集合{A,B}是频繁项集,即A、B同时出现在一条记录的次数大于等于最小支持度min_support,则它的子集{A},{B}出现次数必定大于等于min_support,即它的子集都是频繁项集。
Apriori定律2:如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
举例:假设集合{A}不是频繁项集,即A出现的次数小于 min_support,则它的任何超集如{A,B}出现的次数必定小于min_support,因此其超集必定也不是频繁项集。下图表示当我们发现{A,B}是非频繁集时,就代表所有包含它的超集也是非频繁的,即可以将它们都剪除。
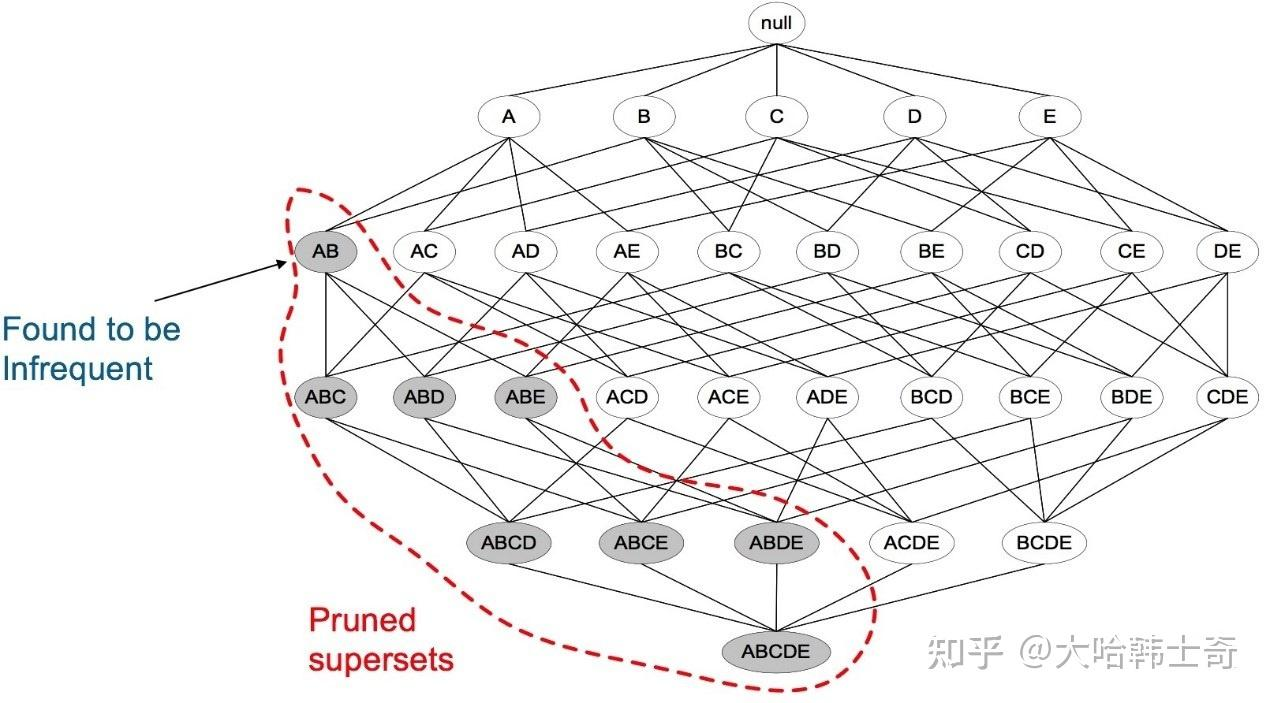
算法的思路:
Apriori算法的目标是找到最大的K项频繁集。这里有两层意思,首先,我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。Apriori算法采用了迭代的方法,先搜索出候选1项集及对应的支持度,剪枝去掉低于支持度的1项集,得到频繁1项集。然后对剩下的频繁1项集进行连接,得到候选的频繁2项集,筛选去掉低于支持度的候选频繁2项集,得到真正的频繁二项集,以此类推,迭代下去,直到无法找到频繁k+1项集为止,对应的频繁k项集的集合即为算法的输出结果。
输入:数据集合D,支持度阈值min_support
输出:最大的频繁k项集
一、扫描整个数据集,得到所有出现过的数据,作为候选频繁1项集。k=1,频繁0项集为空集。
二、挖掘频繁k项集
a) 扫描数据计算候选频繁k项集的支持度
b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空,则直接返回频繁k-1项集的集合作为算法结果,算法结束。如果得到的频繁k项集只有一项,则直接返回频繁k项集的集合作为算法结果,算法结束。
c) 基于频繁k项集,连接生成候选频繁k+1项集。
三、 令k=k+1,转入步骤二。
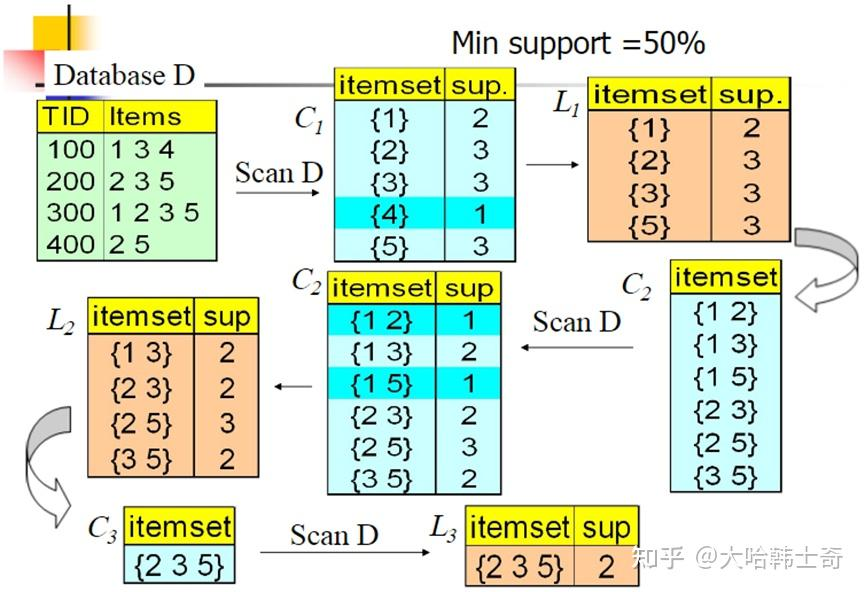
在上面的例子中,数据集D有4条记录,分别是134,235,1235和25。现在我们用Apriori算法来寻找频繁k项集,最小支持度设置为50%。首先我们生成候选频繁1项集,包括我们所有的5个数据并计算5个数据的支持度,计算完毕后我们进行剪枝,数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235,现在我们链接生成候选频繁2项集,包括12,13,15,23,25,35共6组。此时我们的第一轮迭代结束。
进入第二轮迭代,我们扫描数据集计算候选频繁2项集的支持度,接着进行剪枝,由于12和15的支持度只有25%而被筛除,得到真正的频繁2项集,包括13,23,25,35。现在我们链接生成候选频繁3项集,123, 135和235共3组,这部分图中没有画出。通过计算候选频繁3项集的支持度,我们发现123和135的支持度均为25%,因此接着被剪枝,最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接,进而得到候选频繁4项集,最终的结果即为频繁3三项集235。
PCY算法
Apriori算法在效率上有很大的不足,第一遍扫描中可能有大量未用内存空间这一观察结果。
这是Apriori前两遍扫描的内存占用图: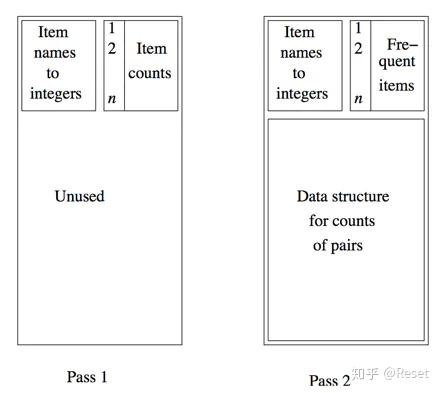
第一遍扫描,左上角是项名称到整数的映射,右边是项的计数值,剩下的空间是不使用的;第二遍扫描,已经筛选掉了支持度不足的项,只保留了足够频繁的频繁项C1,然后对所有可能的C1项进行组合,得到C2的候选,也就是图中下面的部分。
然后是PCY算法前两遍扫描的内存占用图:
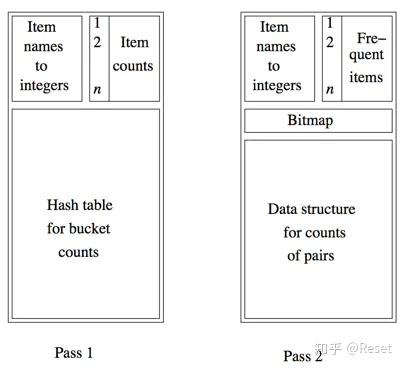
PCY算法在第一遍扫描时对购物篮进行检查,且不仅对篮中的每个项的计数值加1,而且通过一个双重循环生成所有的项对。对每个项对我们将哈希结果对应的桶元素加1,而且项对本身并不会放到哈希桶中,因此它只会影响桶中的单个整数。也就是第一遍扫描时图中下面的部分。
第一遍扫描结束时,每个桶中都有一个计数值,记录的是所有哈希到该桶中的项对的数目之和,如果该桶的计数值高于支持度阈值,那么该桶称为频繁桶,我们很容易知道,频繁桶中的项对不一定是频繁项对,因为一个桶中可能有多个项对,但是非频繁桶中的项对一定不可能是频繁项。图中的bimap每一位表示一个桶,如果该位是个频繁桶,则该位置1。
这样,在第二遍扫描的时候,我们所需要进行支持度验证的项对C2就有了两个条件,组成项对的项都是频繁项,且该项对哈希到一个频繁桶。这第二个条件就是PCY算法和Apriori算法的本质区别。将原来存储内容转换成bitmap,内存占用可以变为原来的\frac{1}{16}。
相应的Apriori-PCY算法代码如下:(采用示例数据集)
import pandas as pd
import re
import time
support = 0.005 # 频繁项集的最小支持度设为0.005
confidence = 0.5 # 关联规则的置信度为0.5
def generateC1(dataset):
C1 = set()
for data in dataset:
for item in data:
itemset = frozenset([item])
C1.add(itemset)
return C1
def isapriori(ckitem, lx):
for item in ckitem:
ck_sub = ckitem - frozenset([item])
if ck_sub not in lx:
return False
return True
def generateCk(lx, k):
Ck = set()
length = len(lx)
listlx = list(lx)
for i in range(length):
for j in range(i, length):
l1 = list(listlx[i])
l2 = list(listlx[j])
l1.sort()
l2.sort()
if l1[0:k-2] == l2[0:k-2]:
ckitem = listlx[i] | listlx[j]
if isapriori(ckitem, lx):
Ck.add(ckitem)
return Ck
def PCY(lx, k, bucket_num=2000):
hash_table = {}
bucketcount = [0 for x in range(0, bucket_num)]
bitmap = [0 for x in range(0, bucket_num)]
pair = set()
Ck = set()
length = len(lx)
listlx = list(lx)
for i in range(length):
for j in range(i, length):
l1 = list(listlx[i])
l2 = list(listlx[j])
l1.sort()
l2.sort()
if l1[0:k-2] == l2[0:k-2]:
ckitem = listlx[i] | listlx[j]
if isapriori(ckitem, lx):
hash_table[ckitem] = (i * j) % bucket_num
bucketcount[hash_table[ckitem]] += 1
pair.add(ckitem)
for i in range(0, len(bucketcount)):
if bucketcount[i] > 0.005 * len(lx):
bitmap[i] = 1
else:
bitmap[i] = 0
for item in pair:
if bitmap[hash_table[item]] == 1:
Ck.add(item)
return Ck
def generateLk(dataset, Ck, min_support, support_data):
item_num = {}
Lk = set()
for data in dataset:
for item in Ck:
if item.issubset(data):
if item not in item_num:
item_num[item] = 1
else:
item_num[item] += 1
sum_lk = float(len(dataset))
for item in item_num:
if (item_num[item] / sum_lk) >= min_support:
Lk.add(item)
support_data[item] = item_num[item] / sum_lk
return Lk
def fre_items(dataset, k, min_support):
support_data = {}
L = []
C1 = generateC1(dataset)
L1 = generateLk(dataset, C1, min_support, support_data)
Lx = L1.copy()
L.append(Lx)
C2 = PCY(Lx, 2)
L2 = generateLk(dataset, C2, min_support, support_data)
Lx = L2.copy()
L.append(Lx)
for i in range(3, k + 1):
Ci = generateCk(Lx, i)
Li = generateLk(dataset, Ci, min_support, support_data)
Lx = Li.copy()
L.append(Lx)
return L, support_data
def generate_big_rules(L, support_data, min_conf):
big_rule_list = []
sub_set_list = []
for i in range(0, len(L)):
for freq_set in L[i]:
for sub_set in sub_set_list:
if sub_set.issubset(freq_set):
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf)
if conf >= min_conf and big_rule not in big_rule_list:
big_rule_list.append(big_rule)
sub_set_list.append(freq_set)
return big_rule_list
if __name__ == '__main__':
# 直接在代码中定义数据集
dataset = [
['milk', 'bread', 'eggs'],
['milk', 'diapers', 'beer', 'eggs'],
['bread', 'butter'],
['milk', 'bread', 'butter', 'eggs'],
['diapers', 'beer'],
['milk', 'diapers', 'beer', 'coke'],
['bread', 'butter', 'eggs'],
['milk', 'bread', 'diapers', 'beer'],
['milk', 'bread', 'eggs'],
['bread', 'eggs']
]
start = time.time()
L, support_data = fre_items(dataset, k=4, min_support=0.005)
big_rules_list = generate_big_rules(L, support_data, min_conf=0.5)
end = time.time()
for Lk in L:
if len(Lk) == 0:
continue
print("=========================================================")
print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport")
print("=========================================================")
for freq_set in Lk:
print(freq_set, support_data[freq_set])
print("Big Rules")
for item in big_rules_list:
print(item[0], "=>", item[1], "conf: ", item[2])
i = 1
for Lk in L:
print("频繁", i, "项数为:", len(Lk))
i = i + 1
print('规则数为:', len(big_rules_list))
print('程序运行时间为', end - start, 's')fp-growth算法解决关联分析问题
由于Apriori-PCY需要多次遍历整个数据集,随着项集长度增加,扫描次数也增加,效率较低且在数据量大或项集较长时,候选项集数量急剧增加,导致内存和计算资源消耗大。因此,为了提高效率、减少内存消耗,避免频繁生成和检测候选项集,通常采用 FP-Growth 算法。FP-Growth 通过构建压缩的 FP-Tree 结构,无需生成候选项集,只需两次扫描数据集,能更高效地挖掘频繁项集,特别适合大规模和稠密数据场景。
下面使用一个例子引出fp-growth算法。下面是一家超市中的购物记录,下面我们使用fp-growth算法来求解各物品之间的关联度和相关性。
| Transaction ID | Item |
|---|---|
| T100 | I1, I2, I5 |
| T200 | I2, I4 |
| T300 | I2, I3 |
| T400 | I1, I2, I4 |
| T500 | I1, I3 |
| T600 | I2, I3 |
| T700 | I1, I3 |
| T800 | I1, I2, I3, I5 |
| T900 | I1, I2, I3, I6 |
FP-growth算法的核心依赖于FP-tree,其基本原理和算法过程如表格所示,
| 步骤 | 说明 |
|---|---|
| Step 1 | 扫描事务数据库,计算单一项的频率(支持度计数) |
| Step 2 | 按频率递减排列,写出频繁项(1项集)的集合 L |
| Step 3 | 构建 FP 树 |
| Step 4 | 利用 FP 树挖掘生成频繁项集 |
首先我们根据这个交易记录,统计各个物品的购物频率,如表格所示:
| Item | Frequency |
|---|---|
| I1 | 6 |
| I2 | 7 |
| I3 | 6 |
| I4 | 2 |
| I5 | 2 |
| I6 | 1 |
我们假定最小支持度的阈值是2,即频率低于2的项集将会自动被剔除,在本例中I6项则会被剔除,按照出现的频率降序排列(对于频率相同的项,我们采用表头字典顺序进行排序),我们便可以得到如下的表格:
| Item | Frequency |
|---|---|
| I2 | 7 |
| I1 | 6 |
| I3 | 6 |
| I4 | 2 |
| I5 | 2 |
接着,我们对这笔账单里物品的顺序按照频率进行降序排列和重组,于是得到如下的表单:
| Transaction ID | Item | ordered Itemset |
|---|---|---|
| T100 | I1, I2, I5 | I2, I1, I5 |
| T200 | I2, I4 | I2, I4 |
| T300 | I2, I3 | I2, I3 |
| T400 | I1, I2, I4 | I2, I1, I4 |
| T500 | I1, I3 | I1, I3 |
| T600 | I2, I3 | I2, I3 |
| T700 | I1, I3 | I1, I3 |
| T800 | I1, I2, I3, I5 | I2, I1, I3, I5 |
| T900 | I1, I2, I3, I6 | I2, I1, I3 |
然后便是最重要的环节——构建FP-Tree,首先创建树的根节点NULL,随后扫描事务数据库,将项集按照上图所示的顺序进行依次添加,针对每一个事务创建一个分支,例如下图所示,代表了{I2,I1,I5}。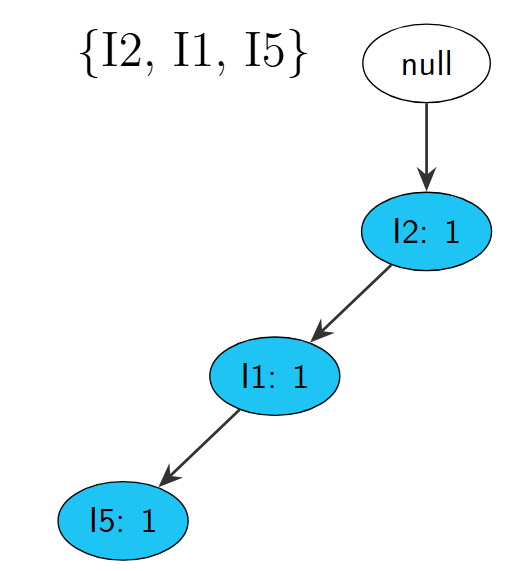
接着依次添加{I2,I4},{I2,I3},{I2,I1,I4},每添加一次,就要在树的节点旁边用数字代表它所出现的频率,由于I2项集目前出现了4次,因此在I2的节点右侧以"冒号:4"的形式代表了它出现的频率,如图所示: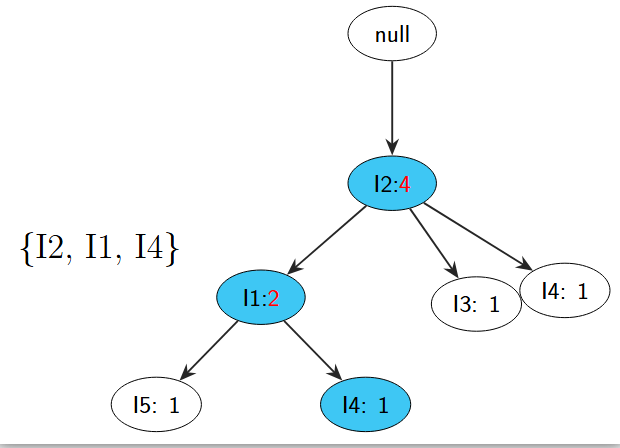
接着在添加下一个项集{I1,I3}时,由于I1项集是直接连接在树根上的,因此需要在I2节点旁再出一个新的节点I1,并接上I3,同时加上频率,如图所示,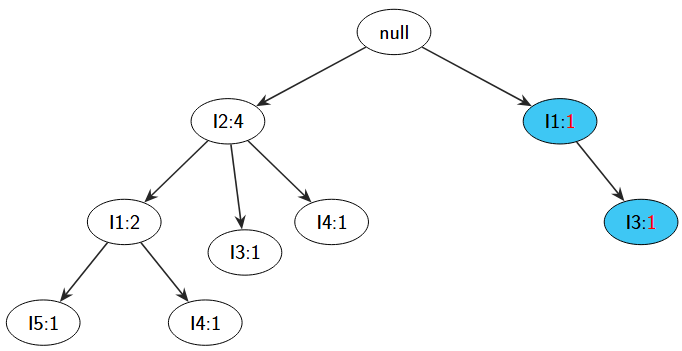
最后在添加完所有的项集之后,我们便可得到如下图所示优美的FP-tree图:
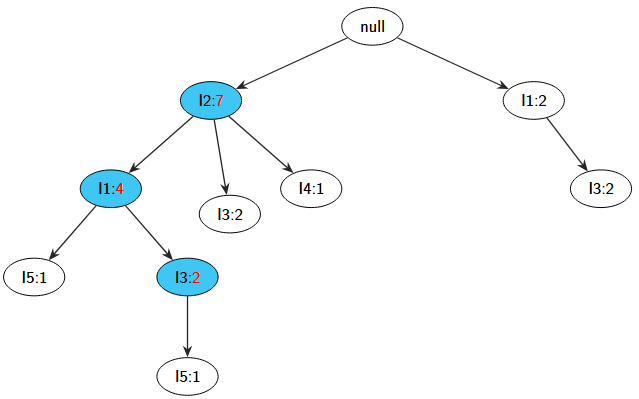
然后创建项头表,使每个项目通过节点链指向它在Tree中的位置,如图所示: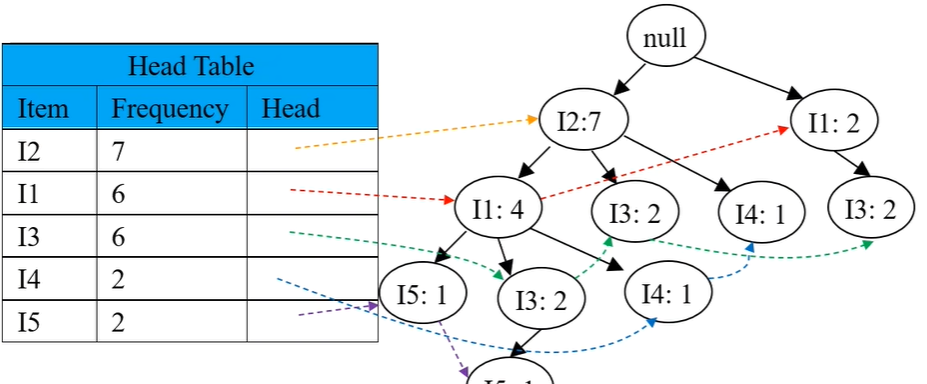
接着使用FP树挖掘生成频繁项集,其基本步骤如下:
对项头表按频率从低到高遍历,构造各个项目(节点)的条件模式基;(条件模式基指的是头部链表中某一节点的前缀路径组合。)
构造条件FP树,要求支持度计数大于等于最小支持度计数
使用条件FP树与叶子节点组合得到频繁项集
在创建FP树的时候是按照频率从上往下创建的,而在利用FP树进行关联分析的搜寻时却是自下而上的!
在进行各项的搜寻后,我们便可得到如下的结果:
| Item | 条件模式基 | 条件 FP 树 | 频繁项集 |
|---|---|---|---|
| I5 | {{I2 II:1},{I2 II I3:1}} | <I2:2, II:2> | {I2 I5:2},{II I5:2},{I2 II I5:2} |
| I4 | {{I2 II:1},{I2:1}} | I2:2 | {I2 I4:2} |
| I3 | {{I2 II:2},{I2:2},{II:2}} | <I2:4, II:2>, II:2 | {I2 I3:4},{II I3:4},{I2 II I3:2} |
| I1 | {{I2:4}} | I2:4 | {I2 I1:4} |
结果这过程的python代码如下:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from collections import defaultdict, Counter
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import fpgrowth
# 设置matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 或 ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 解析事务数据
def parse_transaction_data():
"""
解析事务数据,将图片中的数据转换为Python列表格式
"""
transactions = [
['I1', 'I2', 'I5'], # T100
['I2', 'I4'], # T200
['I2', 'I3'], # T300
['I1', 'I2', 'I4'], # T400
['I1', 'I3'], # T500
['I2', 'I3'], # T600
['I1', 'I3'], # T700
['I1', 'I2', 'I3', 'I5'], # T800
['I1', 'I2', 'I3', 'I6'] # T900
]
transaction_ids = ['T100', 'T200', 'T300', 'T400', 'T500', 'T600', 'T700', 'T800', 'T900']
print("解析的事务数据:")
for tid, items in zip(transaction_ids, transactions):
print(f"{tid}: {', '.join(items)}")
return transactions
# FP-Tree节点类
class FPNode:
def __init__(self, item, count=1, parent=None):
self.item = item # 节点表示的项
self.count = count # 计数
self.parent = parent # 父节点
self.children = {} # 子节点 {item: FPNode}
self.next = None # 相同项的下一个节点(用于项头表)
def increment(self, count=1):
"""增加节点的计数"""
self.count += count
def display(self, ind=1):
"""打印节点信息(用于调试)"""
if self.item is None:
print(' ' * ind, "null")
else:
print(' ' * ind, self.item, ':', self.count)
for child in self.children.values():
child.display(ind + 1)
# FP-Growth算法实现
class FPGrowth:
def __init__(self, min_support=0.2):
self.min_support = min_support
self.header_table = defaultdict(lambda: [0, None]) # 项头表 {item: [count, node]}
self.root = FPNode(None) # 创建FP-Tree的根节点
self.transactions = [] # 存储事务数据
def fit(self, transactions):
"""构建FP-Tree并挖掘频繁项集"""
self.transactions = transactions
# 第一次扫描:计算每个项的支持度
item_counts = Counter([item for transaction in transactions for item in transaction])
n_transactions = len(transactions)
# 过滤不满足最小支持度的项
min_count = self.min_support * n_transactions
self.frequent_items = {}
# 按支持度降序排列频繁项
for item, count in sorted(item_counts.items(), key=lambda x: (-x[1], x[0])):
if count >= min_count:
self.frequent_items[item] = count
# 如果没有频繁项,则返回空
if not self.frequent_items:
return {}
# 更新项头表的计数
for item, count in self.frequent_items.items():
self.header_table[item][0] = count
# 第二次扫描:构建FP-Tree
for transaction in transactions:
# 过滤非频繁项并按支持度排序
filtered_items = [item for item in transaction if item in self.frequent_items]
# 按照频繁项的顺序排序(支持度降序)
filtered_items.sort(key=lambda x: list(self.frequent_items.keys()).index(x))
if filtered_items:
self._insert_tree(filtered_items, self.root)
return self.header_table
def _insert_tree(self, items, node):
"""将排序后的项插入FP-Tree"""
if not items:
return
item = items[0]
# 检查当前节点的子节点中是否已存在该项
if item in node.children:
node.children[item].increment()
else:
# 创建新节点
new_node = FPNode(item, 1, node)
node.children[item] = new_node
# 更新项头表
if self.header_table[item][1] is None:
self.header_table[item][1] = new_node
else:
self._update_header_table(item, new_node)
# 递归插入剩余项
self._insert_tree(items[1:], node.children[item])
def _update_header_table(self, item, new_node):
"""更新项头表,将新节点添加到链表末尾"""
current = self.header_table[item][1]
while current.next is not None:
current = current.next
current.next = new_node
def get_support(self, item_set):
"""计算项集的支持度"""
if not item_set:
return 0
# 使用mlxtend库计算支持度
te = TransactionEncoder()
te_ary = te.fit_transform(self.transactions)
df = pd.DataFrame(te_ary, columns=te.columns_)
# 使用fpgrowth函数计算频繁项集
frequent_itemsets = fpgrowth(df, min_support=0, use_colnames=True)
# 查找指定项集的支持度
for _, row in frequent_itemsets.iterrows():
if set(row['itemsets']) == set(item_set):
return row['support']
return 0
def visualize_fp_tree(self):
"""可视化FP-Tree"""
G = nx.DiGraph()
# 添加根节点
G.add_node("null")
# 递归添加节点和边
node_id_map = {} # 用于跟踪节点ID
def add_nodes_edges(node, parent_id):
if node.item is None:
return
# 为每个节点创建唯一ID
node_id = f"{node.item}:{node.count}"
if node_id in node_id_map:
# 如果ID已存在,添加唯一标识符
count = 1
while f"{node_id} ({count})" in node_id_map:
count += 1
node_id = f"{node_id} ({count})"
# 记录节点ID
node_id_map[node_id] = node
# 添加节点
G.add_node(node_id)
# 添加边
G.add_edge(parent_id, node_id)
# 递归处理子节点
for child in node.children.values():
add_nodes_edges(child, node_id)
# 从根节点的子节点开始添加
for child in self.root.children.values():
add_nodes_edges(child, "null")
# 设置节点颜色
node_colors = []
# 标记主要路径节点为蓝色
for node in G.nodes():
if node == "null":
node_colors.append("white")
elif node.startswith("I2:7") or node.startswith("I1:4") or (node.startswith("I3:2") and len(list(G.successors(node))) > 0):
node_colors.append("lightblue")
else:
node_colors.append("white")
# 绘制图形
plt.figure(figsize=(10, 8))
# 使用spring布局代替graphviz布局
pos = nx.spring_layout(G, seed=42)
# 绘制节点
nx.draw_networkx_nodes(G, pos, node_size=1500, node_color=node_colors, edgecolors="black")
# 绘制边和箭头
nx.draw_networkx_edges(G, pos, width=1.0, arrowsize=15, arrowstyle='->')
# 绘制标签
nx.draw_networkx_labels(G, pos, font_size=10)
plt.title('FP-Tree结构')
plt.axis('off')
plt.tight_layout()
plt.savefig('corrected_fp_tree.png', dpi=300, bbox_inches='tight')
plt.close()
print("修正后的FP-Tree可视化已保存为 'corrected_fp_tree.png'")
# 打印树结构(用于调试)
print("\nFP-Tree结构:")
self.root.display(0)
# 主函数
def main():
# 解析事务数据
transactions = parse_transaction_data()
# 设置最小支持度
min_support = 0.2 # 20%
# 创建FP-Growth对象并构建FP-Tree
fp_growth = FPGrowth(min_support)
header_table = fp_growth.fit(transactions)
# 打印项头表(包含支持度)
print("\n项头表(包含支持度):")
for item, (count, _) in sorted(header_table.items(), key=lambda x: (-x[1][0], x[0])):
support = count / len(transactions)
print(f"{item}: 计数={count}, 支持度={support:.2f}")
# 可视化FP-Tree
fp_growth.visualize_fp_tree()
# 使用mlxtend库计算频繁项集
te = TransactionEncoder()
te_ary = te.fit_transform(transactions)
df = pd.DataFrame(te_ary, columns=te.columns_)
# 使用fpgrowth函数计算频繁项集
frequent_itemsets = fpgrowth(df, min_support=min_support, use_colnames=True)
# 打印频繁项集
print("\n频繁项集(支持度 >= 0.2):")
for _, row in frequent_itemsets.iterrows():
items = list(row['itemsets'])
support = row['support']
print(f"{items}: 支持度={support:.2f}")
if __name__ == "__main__":
main()最后代码会输出我们的fp-tree图和以下的关联性数据
| 项集 | 支持度 |
|---|---|
| ['I2'] | 0.78 |
| ['I1'] | 0.67 |
| ['I3'] | 0.67 |
| ['I5'] | 0.22 |
| ['I4'] | 0.22 |
| ['I1', 'I2'] | 0.44 |
| ['I2', 'I3'] | 0.44 |
| ['I3', 'I1'] | 0.44 |
| ['I1', 'I5'] | 0.22 |
| ['I2', 'I5'] | 0.22 |
| ['I2', 'I4'] | 0.22 |
| ['I2', 'I1', 'I5'] | 0.22 |
| ['I2', 'I3', 'I1'] | 0.22 |
忽略1-项集,假设最小支持度的阈值为20%,我们便可得到I1与I2,I2与I3等等之间存在极大的关联性。
总之,FP-Growth算法成功地从给定事务数据中挖掘出了频繁项集,并计算了各个物品及其组合的支持度。通过FP-Tree的可视化,我们可以直观地了解物品之间的关联关系,这对于进行关联规则挖掘和推荐系统构建具有重要价值。
FP-Growth算法的核心优势在于其高效性:通过将频繁项按照支持度降序排列,构建紧凑的树结构,避免了Apriori算法中的候选集生成和测试过程,大大提高了频繁项集挖掘的效率。


