
相比于K-means需要事先指定k值且只能找到球形或凸形聚类、易将所有点分配到某个聚类,容易受异常值影响的缺点,DBscan由于考虑到了噪声点的影响,因此能够更好地完成聚类的任务。一般来说,当待分类的数据中,包含噪声数据,聚类形状不规则或者不知道聚类的具体数量的时候,我们常采用的是DBSCAN,而不是K-means算法。
DBSCAN的算法原理
DBscan的原理与k-means的单纯距离论有着显著的区别。我们首先需要定义簇的定义:密度相连的点的最大集合。将其看作是数据空间中被低密度区域(代表噪声)分割开的稠密对象区域。
定义邻域:给定对象半径 ε (Eps, epsilon) 内的邻域称为该对象的 ε 邻域\{p \text{ belongs to } D | \text{dist}(p,q) \leq \text{Eps}\}
定义密度:给定距离内最小的对象点数目 (MinPts)
定义高密度:一个对象的邻域至少包含最小数目 MinPts 个对象|N_{\text{Eps}}(p)| \geq \text{MinPts}
定义核心对象:如果对象的邻域至少包含最小数目 MinPts 的对象,则称该对象为核心对象。
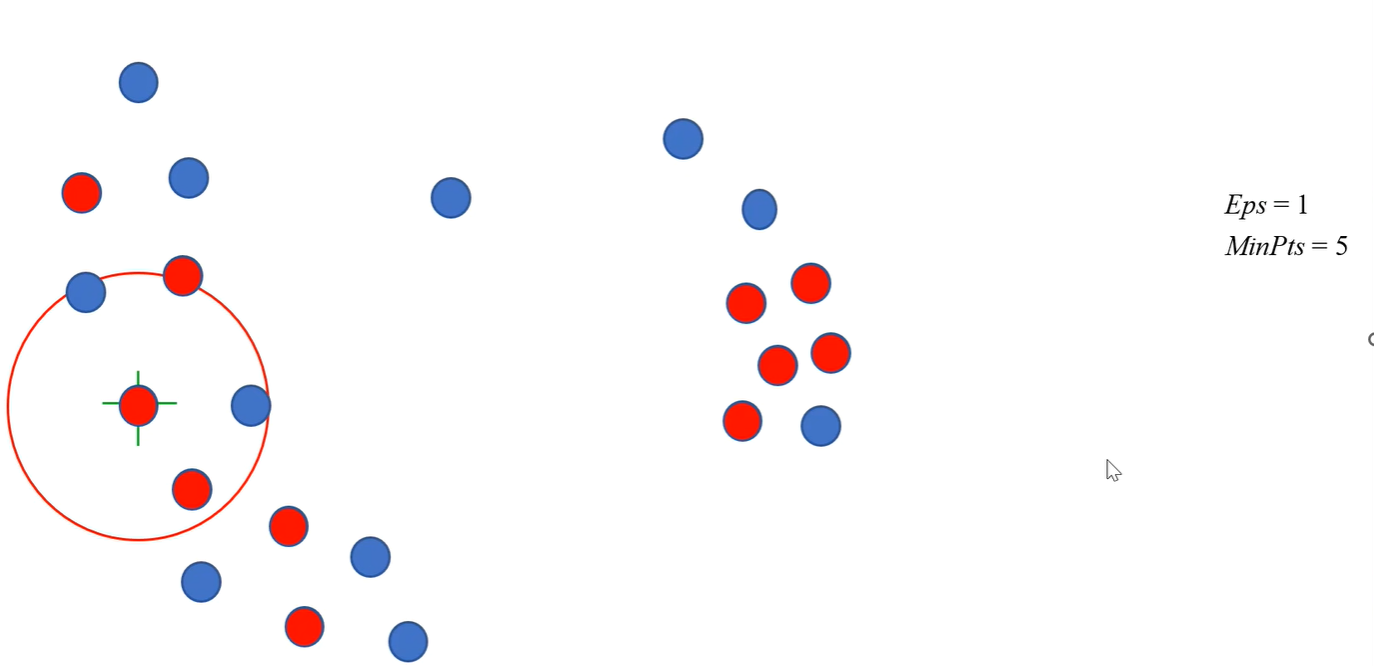
例如在给定的半径为1,最小密度为5的前提下,被标红的为核心对象,而在蓝色的点中,还包含了一些低密度和中等密度的点,他们不能被我们当成噪声而一概而论,需要我们令加讨论:
定义边界对象:对象的邻域小于 MinPts 个对象,但是在一个核心对象的邻域中。
定义离群点/噪声:对象的邻域小于 MinPts 个对象,且不是边界点。
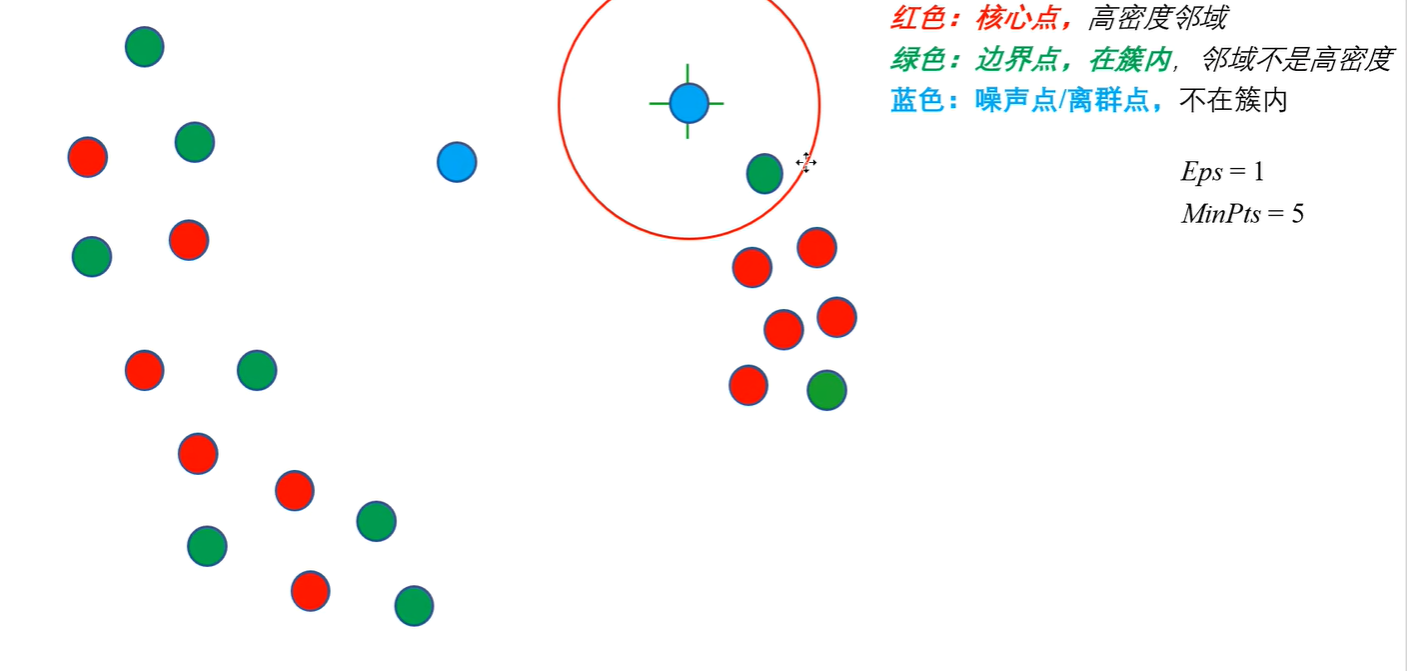
例如在上图中,蓝色的点就是噪声点,而绿色的则是被认为是低密度的边界点。
定义直接密度可达:给定一个对象集合 D,如果 p 在 q 的邻域内,而 q 是一个核心对象,则我们说对象 p 从对象 q 出发是直接密度可达的。
定义密度可达:
如果存在一个对象链 p_1, p_2, \ldots, p_n 满足:
则称 p是从 q 关于 \varepsilon 和 \text{MinPts} 密度可达的。
定义密度相连:如果存在一个对象o \in D,使得:
则称p 是从q 关于\varepsilon 和\text{MinPts} 密度相连的。
例如在上述的例子当中:
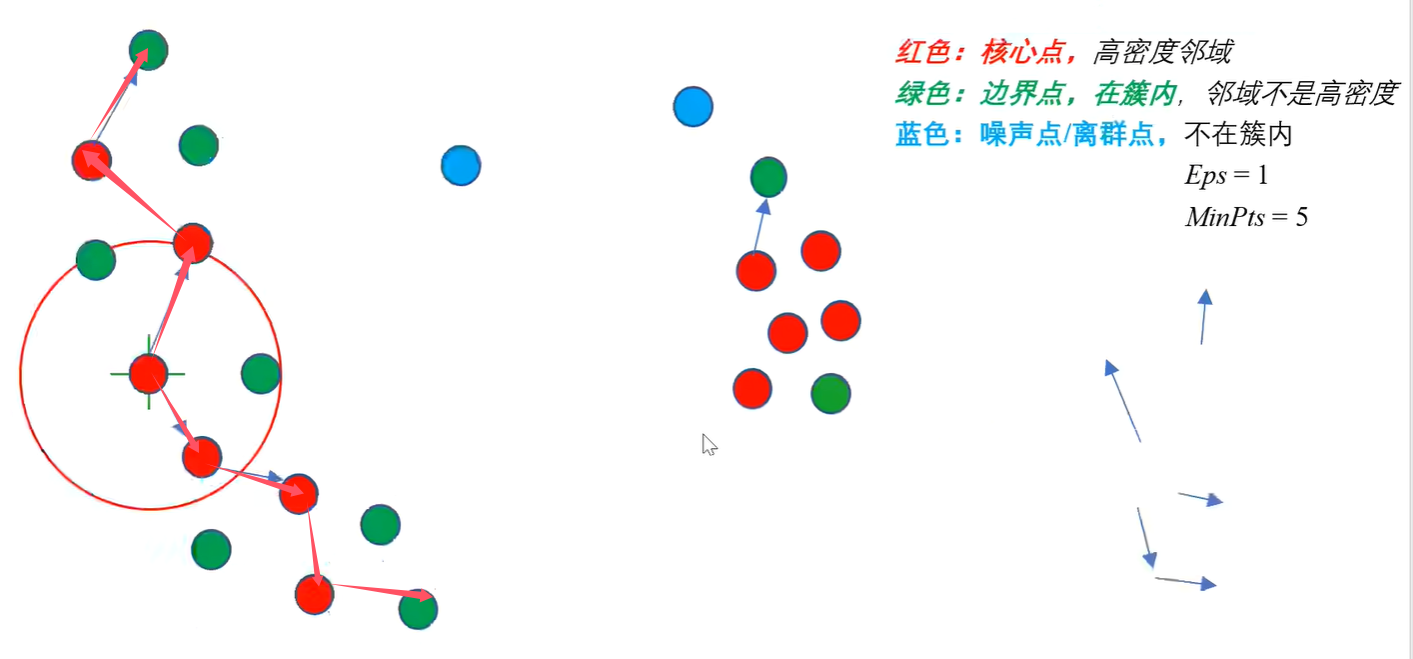
如图所示以中心的标红的点为中心,分别向上和向下延伸,即可构造出如图标红的一个簇,这个簇中的点都是密度相连的。
DBscan发现簇的算法原理
DBSCAN 通过检查数据库中每点的邻域来搜索簇。如果点p的邻域包含的点多于 MinPts 个,则创建一个以 p 为核心对象的新簇。 然后,DBSCAN 迭代地聚集从这些核心对象密度可达的对象,这个过程可能涉及一些密度可达簇的合并。当没有新的点可以添加到任何簇时,该过程结束。从剩余的对象中随机选择下一个未访问对象,重复3)的过程,直到所有对象都被访问。
由此可见,DBSCAN 最大的优势是可以发现任意形状的聚类簇,而不是像 K-Means,一般仅仅用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点。
一般来说,如果数据集是稠密的,并且数据集不是凸的,那么用 DBSCAN 会比 K-Means 聚类效果好很多。如果数据集不是稠密的,则不推荐用 DBSCAN 来聚类。
在这里可以体验DBSCAN算法在各种实际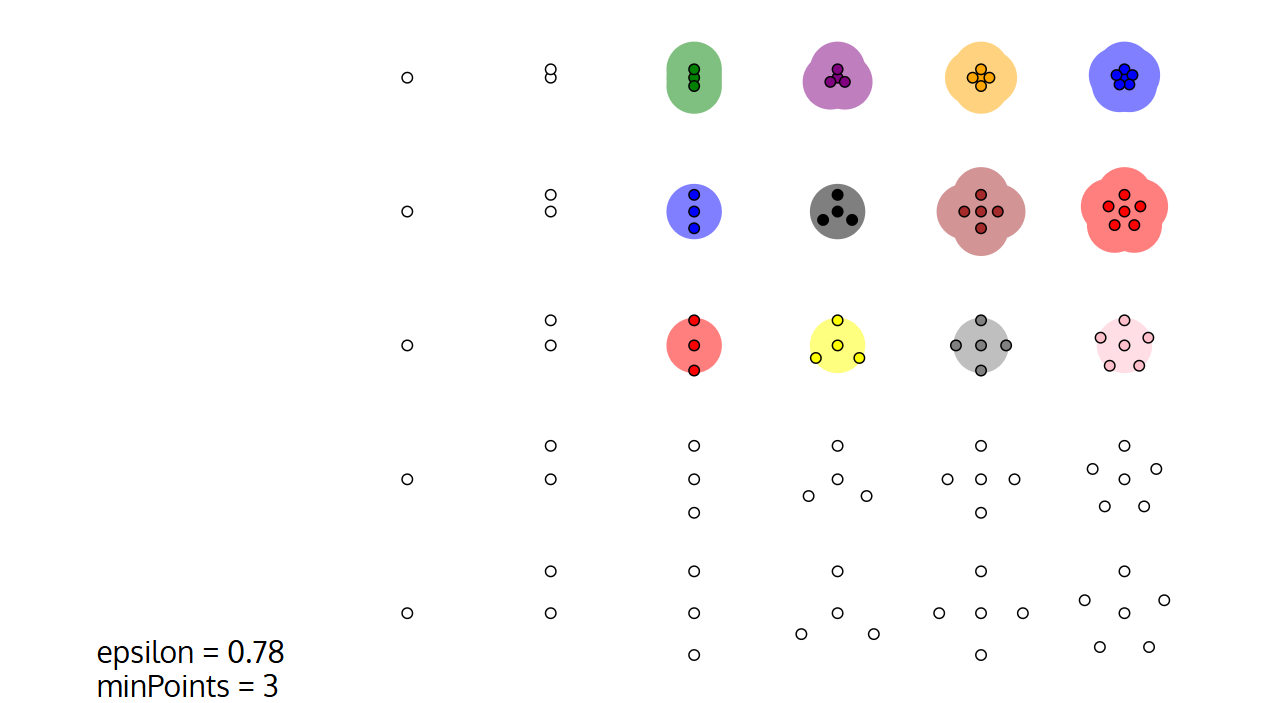


DBSCAN的调参
最简单和朴素的调参方式:
k值的选取:一般建议k等于2*维度-1,其中的维度指的也就是特征值,例如,有2个指标,则k的值应当为2*2-1=3.
计算并绘制k-distance图,计算出每一个点到距离其第k个近的点的距离,然后讲这些点的距离从大到小后进行排序并绘图:
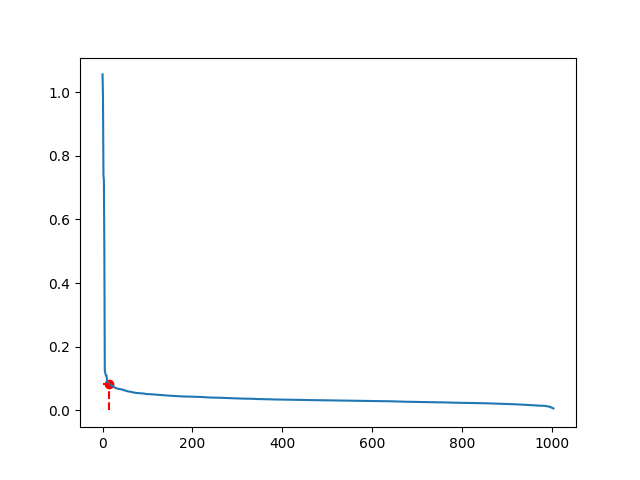 根据肘部原理,图中被标记成红色的点就是拐点位置,这时他的距离(distance,即纵轴坐标)就是\varepsilon 的值
根据肘部原理,图中被标记成红色的点就是拐点位置,这时他的距离(distance,即纵轴坐标)就是\varepsilon 的值minpts的取值:MinPts的值一般就是k值加1,即MinPts=k+1.(因为k是距离点p第k近的点,那点p以这个距离为半径的邻域里就有k+1个点)
此过程的代码示例:
import numpy as np
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
np.random.seed(2021)
data = np.ones([1005,2])
data[:1000] = make_moons(n_samples=1000,noise=0.05,random_state=2022)[0]
data[1000:] = [[-1,-0.5],
[-0.5,-1],
[-1,1.5],
[2.5,-0.5],
[2,1.5]]
print(data.shape)
plt.scatter(data[:,0],data[:,1],color="c")
plt.show()
def select_MinPts(data,k):
k_dist = []
for i in range(data.shape[0]):
dist = (((data[i] - data)**2).sum(axis=1)**0.5)
dist.sort()
k_dist.append(dist[k])
return np.array(k_dist)
k = 3 # 此处k取 2*2 -1
k_dist = select_MinPts(data,k)
k_dist.sort()
plt.plot(np.arange(k_dist.shape[0]),k_dist[::-1])
# 由拐点确定邻域半径
eps = k_dist[::-1][15]
plt.scatter(15,eps,color="r")
plt.plot([0,15],[eps,eps],linestyle="--",color = "r")
plt.plot([15,15],[0,eps],linestyle="--",color = "r")
plt.show()
dbscan_model = DBSCAN(eps=eps,min_samples=k+1)
label = dbscan_model.fit_predict(data)
print(label)
class_1 = []
class_2 = []
noise = []
for index,value in enumerate(label):
if value == 0:
class_1.append(index)
elif value == 1:
class_2.append(index)
elif value == -1:
noise.append(index)
plt.scatter(data[class_1,0],data[class_1,1],color="g",label="class 1")
plt.scatter(data[class_2,0],data[class_2,1],color="b",label = "class 2")
plt.scatter(data[noise,0],data[noise,1],color="r",label = "noise")
plt.legend()
plt.show()
聚类的结果如图所示: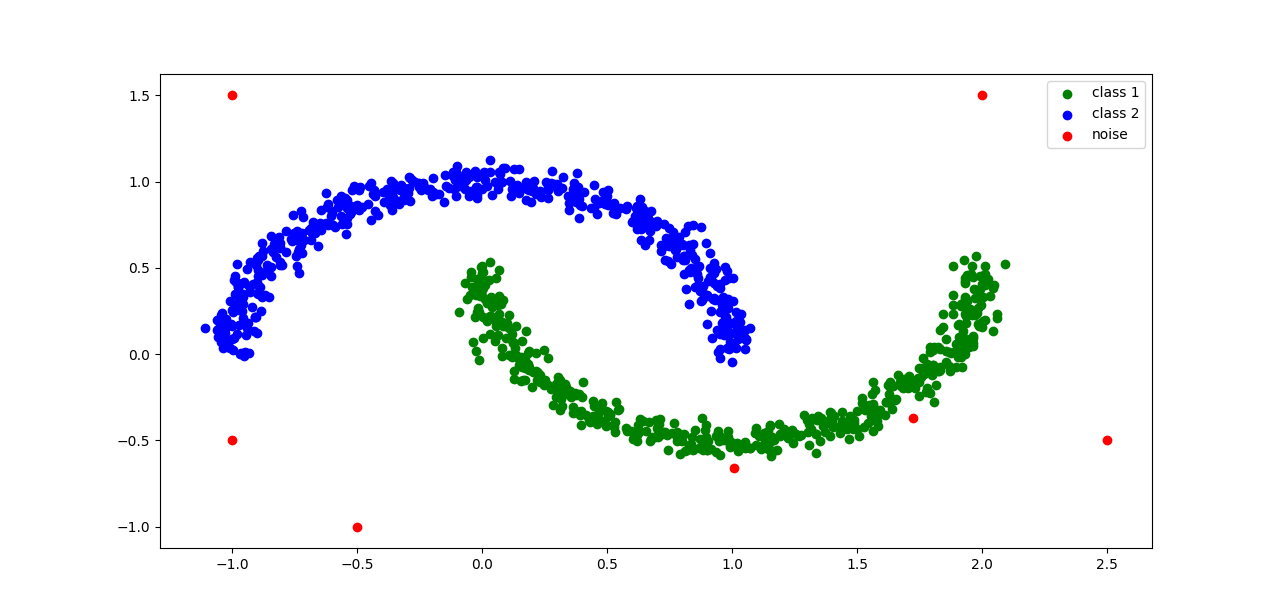
可视化的自动调参:(不断履历不同的\varepsilon 和MinPts评估不同情况下的优劣性)
首先需要定义两个用于评判分类良好与否的标准——轮廓系数和噪声比
轮廓系数:轮廓系数是衡量聚类效果好坏的一种指标。它结合了聚类的凝聚度(cohesion)和分离度(separation)。
对于数据集中的每个样本点
i,轮廓系数s(i)的计算公式如下:s(i) = (b(i) - a(i)) / max(a(i), b(i))其中:
a(i):样本点i到其所在簇内所有其他点的平均距离(衡量凝聚度,值越小越好)。b(i):样本点i到与其最近的相邻簇(即不包含i的其他簇)中所有点的平均距离(衡量分离度,值越大越好)。轮廓系数的取值范围是 [-1, 1]:接近 1:表示样本点与自身簇的匹配度高,与相邻簇的匹配度低,聚类效果好。
接近 0:表示样本点位于两个簇的边界上,可能被错误地分配到当前簇。
接近 -1:表示样本点更适合被分配到相邻簇,而不是当前簇,聚类效果差。此时会出现聚类错误或者失败的情况
整个数据集的轮廓系数是所有样本点轮廓系数的平均值。
一般而言噪声点的轮廓系数就是0!
噪声比:噪声比是衡量数据集中被识别为噪声点的比例。在DBSCAN聚类算法中,被标记为
-1的样本点被认为是噪声点(或离群点),不属于任何一个簇。噪声比的计算公式如下:
噪声比 = (被标记为噪声点的数量) / (数据集中总样本点的数量)
这里以随机创建60个数据点为例进行说明,
其数据集如下:
数据集坐标表
| 序号 | X坐标 | Y坐标 |
|---|---|---|
| 1 | -2.68420713 | 1.46973290 |
| 2 | -2.71539062 | -0.76300583 |
| 3 | -2.88981954 | -0.61805525 |
| 4 | -2.74643720 | -1.40005944 |
| 5 | -2.72859298 | 1.50266052 |
| 6 | -2.27989736 | 3.36502220 |
| 7 | -2.82089068 | -0.36947030 |
| 8 | -2.62648199 | 0.76682408 |
| 9 | -2.88795857 | -2.56859114 |
| 10 | -2.67384469 | -0.48011265 |
| 11 | -2.50652679 | 2.93370755 |
| 12 | -2.61314272 | 0.09684284 |
| 13 | -2.78743398 | -1.02483086 |
| 14 | -3.22520045 | -2.26475960 |
| 15 | -2.64354322 | 5.33787705 |
| 16 | -2.38386932 | 6.05139453 |
| 17 | -2.62252620 | 3.68140352 |
| 18 | -2.64832273 | 1.43611502 |
| 19 | -2.19907796 | 3.95659841 |
| 20 | -2.58734619 | 2.34213138 |
| 21 | 1.28479459 | 3.08447636 |
| 22 | 0.93241075 | 1.43639141 |
| 23 | 1.46406132 | 2.26885424 |
| 24 | 0.18096721 | -3.71521773 |
| 25 | 1.08713449 | 0.33925676 |
| 26 | 0.64043675 | -1.87795566 |
| 27 | 1.09522371 | 1.27751045 |
| 28 | -0.75146714 | -4.50498380 |
| 29 | 1.04329778 | 1.03030610 |
| 30 | -0.01019007 | -3.24258692 |
| 31 | -0.51108620 | -5.68121378 |
| 32 | 0.51109806 | -0.46027850 |
| 33 | 0.26233576 | -2.46551985 |
| 34 | 0.98404455 | -0.55962189 |
| 35 | -0.17486400 | -1.13317007 |
| 36 | 0.92757294 | 2.10706295 |
| 37 | 0.65959279 | -1.58389331 |
| 38 | 0.23454059 | -1.49364824 |
| 39 | 0.94236171 | -2.43820017 |
| 40 | 0.04324640 | -2.61670253 |
| 41 | 4.53172698 | -0.05329008 |
| 42 | 3.41407223 | -2.58716277 |
| 43 | 4.61648461 | 1.53870881 |
| 44 | 3.97081495 | -0.81506561 |
| 45 | 4.34975798 | -0.18847148 |
| 46 | 5.39687992 | 2.46225623 |
| 47 | 2.51938325 | -5.36108261 |
| 48 | 4.93200510 | 1.58569655 |
| 49 | 4.31967279 | -1.10496677 |
| 50 | 4.91813423 | 3.51171284 |
| 51 | 3.66193495 | 1.08917280 |
| 52 | 3.80234045 | -0.97269575 |
| 53 | 4.16537886 | 0.96876126 |
| 54 | 3.34459422 | -3.49386944 |
| 55 | 3.58526730 | -2.42688173 |
| 56 | 3.90474358 | 0.53468546 |
| 57 | 3.94924878 | 0.18328617 |
| 58 | 5.48876538 | 5.27195043 |
| 59 | 5.79468686 | 1.13969507 |
| 60 | 3.29832982 | -3.42456273 |
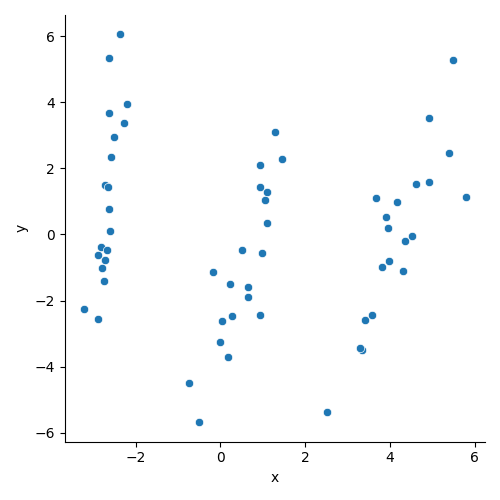
首先导入必要的库:
# 导入必要的库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import DBSCAN
from sklearn import metrics网格搜索参数优化:
设置预定的范围和步长
eps = np.arange(0.2,4,0.2) # eps从0.2到4,步长0.2
min_samples=np.arange(2,20,1) # min_samples从2到20,步长1接下来是这一部分的核心代码;
for i in eps:
for j in min_samples:
try:
db = DBSCAN(eps=i, min_samples=j).fit(data)
labels= db.labels_
k=metrics.silhouette_score(data,labels) # 计算轮廓系数
raito = len(labels[labels[:] == -1]) / len(labels) # 噪声比例
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) # 聚类数量
rs.append([i,j,k,raito,n_clusters_])
# 记录最佳轮廓系数对应的参数
if k>best_score:
best_score=k
best_score_eps=i
best_score_min_samples=j
except:
pass # 处理可能的异常情况随后绘制气泡图将结果进行可视化阐述:
# 以轮廓系数为气泡大小的参数关系图
sns.relplot(x="eps",y="min_samples", size="score",data=rs)
# 以噪声比例为气泡大小的参数关系图
sns.relplot(x="eps",y="min_samples", size="raito",data=rs)如图所示:
轮廓系数图:得分越高越好!,气泡越大!
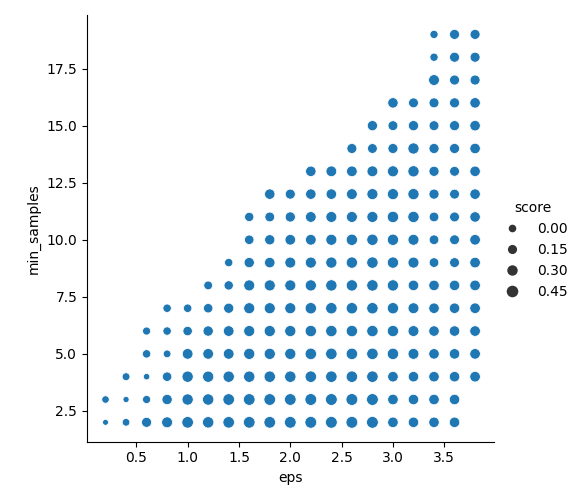
以及接下来的噪声比的图:很明显,噪声比应当越小越好,因此在图中噪声比的值越小,气泡越大,越是我们应当选取的\varepsilon 和MinPts
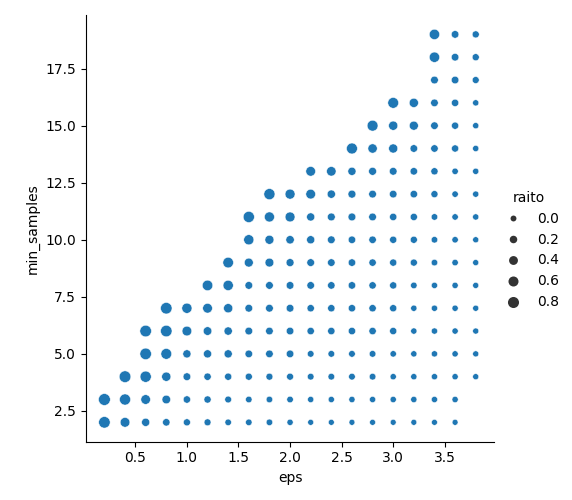
从两张图中,我们可以发现轮廓系数的得分图几乎读不出来任何有用的信息,这是因为他们彼此之间的区分度太小了,而我们注意到噪声比的图中出现较大缺口:可以发现当\varepsilon 取0.7左右,MinPts取7左右时,噪声比是相对较小的,因此我们采用的这个作为被优化之后的参数,并在修改代码中的参数:
db = DBSCAN(eps=2.2, min_samples=7).fit(data)继续运行python代码,我们可以得到如下的分类结果图:
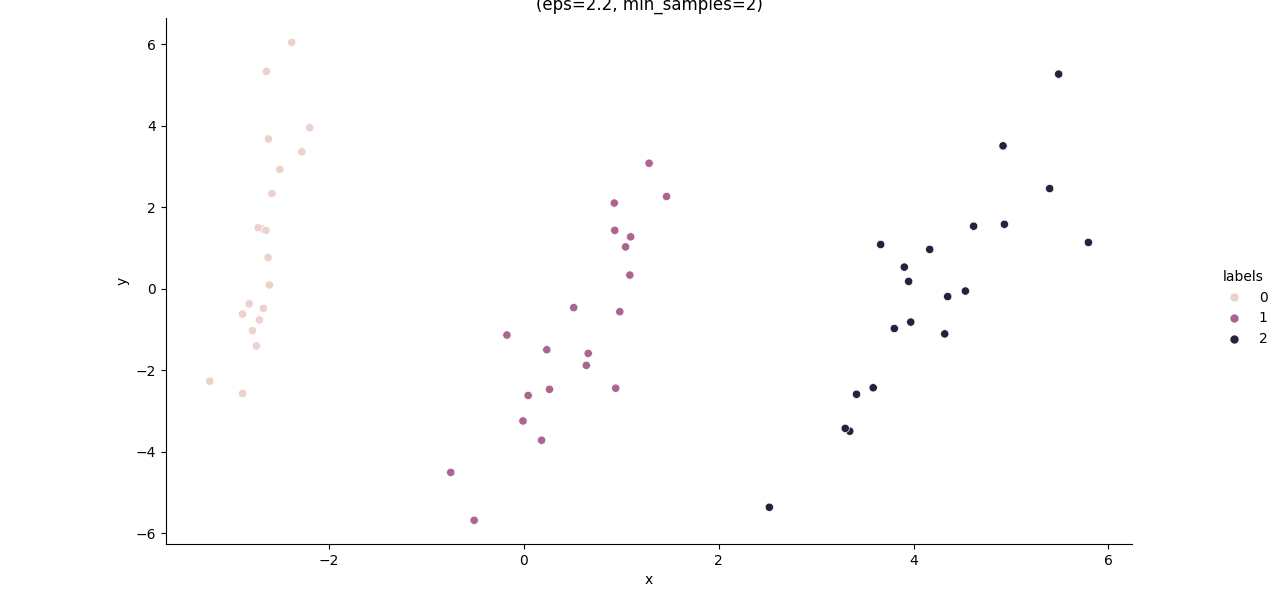
此过程完整的python代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# 数据定义
data = [
[-2.68420713,1.469732895],[-2.71539062,-0.763005825],[-2.88981954,-0.618055245],[-2.7464372,-1.40005944],[-2.72859298,1.50266052],
[-2.27989736,3.365022195],[-2.82089068,-0.369470295],[-2.62648199,0.766824075],[-2.88795857,-2.568591135],[-2.67384469,-0.48011265],
[-2.50652679,2.933707545],[-2.61314272,0.096842835],[-2.78743398,-1.024830855],[-3.22520045,-2.264759595],[-2.64354322,5.33787705],
[-2.38386932,6.05139453],[-2.6225262,3.681403515],[-2.64832273,1.436115015],[-2.19907796,3.956598405],[-2.58734619,2.34213138],
[1.28479459,3.084476355],[0.93241075,1.436391405],[1.46406132,2.268854235],[0.18096721,-3.71521773],[1.08713449,0.339256755],
[0.64043675,-1.87795566],[1.09522371,1.277510445],[-0.75146714,-4.504983795],[1.04329778,1.030306095],[-0.01019007,-3.242586915],
[-0.5110862,-5.681213775],[0.51109806,-0.460278495],[0.26233576,-2.46551985],[0.98404455,-0.55962189],[-0.174864,-1.133170065],
[0.92757294,2.107062945],[0.65959279,-1.583893305],[0.23454059,-1.493648235],[0.94236171,-2.43820017],[0.0432464,-2.616702525],
[4.53172698,-0.05329008],[3.41407223,-2.58716277],[4.61648461,1.538708805],[3.97081495,-0.815065605],[4.34975798,-0.188471475],
[5.39687992,2.462256225],[2.51938325,-5.361082605],[4.9320051,1.585696545],[4.31967279,-1.104966765],[4.91813423,3.511712835],
[3.66193495,1.0891728],[3.80234045,-0.972695745],[4.16537886,0.96876126],[3.34459422,-3.493869435],[3.5852673,-2.426881725],
[3.90474358,0.534685455],[3.94924878,0.18328617],[5.48876538,5.27195043],[5.79468686,1.139695065],[3.29832982,-3.42456273]
]
data = pd.DataFrame(data)
data.columns=["x","y"]
sns.relplot(x="x",y="y",data=data)
plt.show()
db = DBSCAN(eps=1, min_samples=5).fit(data)
data["labels"] = db.labels_
labels = db.labels_
raito = data.loc[data["labels"]==-1].x.count()/data.x.count()
print("噪声比:", format(raito, ".2%"))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
print("分簇的数目: %d" % n_clusters_)
print("轮廓系数: %0.3f" % metrics.silhouette_score(data, labels))
sns.relplot(x="x",y="y", hue="labels",data=data)
plt.show()
rs= []
eps = np.arange(0.2,4,0.2)
min_samples=np.arange(2,20,1)
best_score=0
best_score_eps=0
best_score_min_samples=0
for i in eps:
for j in min_samples:
try:
db = DBSCAN(eps=i, min_samples=j).fit(data)
labels= db.labels_
k=metrics.silhouette_score(data,labels)
raito = len(labels[labels[:] == -1]) / len(labels)
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
rs.append([i,j,k,raito,n_clusters_])
if k>best_score:
best_score=k
best_score_eps=i
best_score_min_samples=j
except:
db=""
else:
db=""
rs= pd.DataFrame(rs)
rs.columns=["eps","min_samples","score","raito","n_clusters"]
sns.relplot(x="eps",y="min_samples", size="score",data=rs)
plt.show()
sns.relplot(x="eps",y="min_samples", size="raito",data=rs)
plt.show()
db = DBSCAN(eps=0.7, min_samples=7).fit(data)
data["labels"] = db.labels_
labels = db.labels_
raito = data.loc[data["labels"]==-1].x.count()/data.x.count()
print("噪声比:", format(raito, ".2%"))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
print("分簇的数目: %d" % n_clusters_)
print("轮廓系数: %0.3f" % metrics.silhouette_score(data, labels))
sns.relplot(x="x",y="y", hue="labels",data=data)
plt.show()


